AVL Tree
An AVL tree is a self-balancing form of a binary search tree, in which the height of subtrees differ at most by only 1.
A binary tree is balanced when its left and right subtrees contain roughly the same number of nodes. That is what makes searching the tree really fast. But if a binary search tree is unbalanced, searching can become really slow.
This is an example of an unbalanced tree:
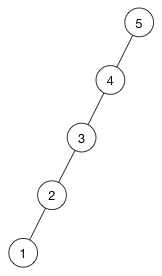
All the children are in the left branch and none are in the right. This is essentially the same as a linked list. As a result, searching takes O(n) time instead of the much faster O(log n) that you’d expect from a binary search tree.
A balanced version of that tree would look like this:
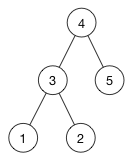
One way to make the binary search tree balanced is to insert the nodes in a totally random order. But that doesn’t guarantee success, nor is it always practical.
The other solution is to use a self-balancing binary tree. This type of data structure adjusts the tree to keep it balanced after you insert or delete nodes. The height of such a tree is guaranteed to be log(n) where n is the number nodes. On a balanced tree all insert, remove, and search operations take only O(log n) time. That means fast. ;-)
Introducing the AVL tree
An AVL tree fixes any imbalances by “rotating” the tree to the left or right.
A node in an AVL tree is considered balanced if its subtrees differ in “height” by at most 1. The tree itself is balanced if all its nodes are balanced.
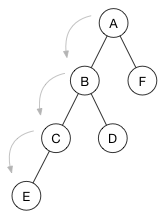
The height of a node is how many steps it takes to get to that node’s lowest leaf. For example, in the following tree it takes three steps to go from A to E, so the height of A is 3. The height of B is 2, the height of C is 1, and the height of the others is 0 because they are leaf nodes.
As mentioned, in an AVL tree a node is balanced if its left and right subtree have the same height. It doesn’t have to be the exact same height, but the difference may not be greater than 1. These are all examples of balanced trees:
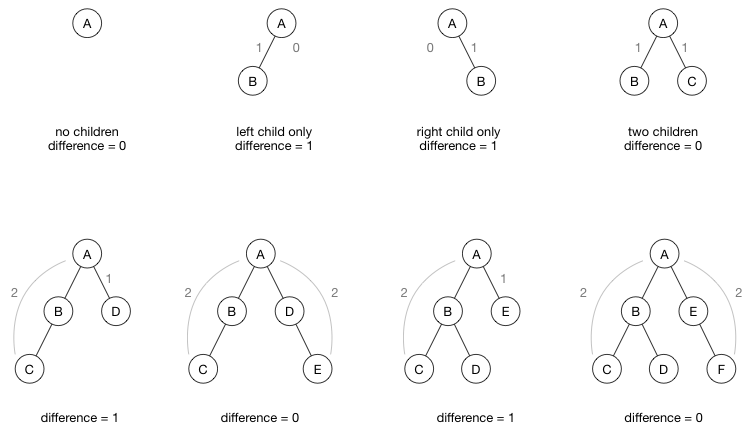
But the following are trees that are unbalanced, because the height of the left subtree is too large compared to the right subtree:
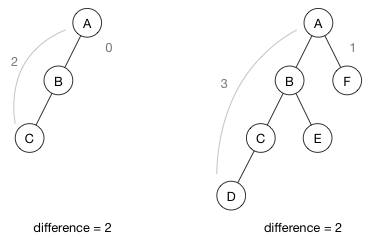
The difference between the heights of the left and right subtrees is called the balance factor. It is calculated as follows:
balance factor = abs(height(left subtree) - height(right subtree))
If after an insertion or deletion the balance factor becomes greater than 1, then we need to re-balance this part of the AVL tree. And that is done with rotations.
Rotations
Each tree node keeps track of its current balance factor in a variable. After inserting a new node, we need to update the balance factor of its parent node. If that balance factor becomes greater than 1, we “rotate” part of that tree to restore the balance.
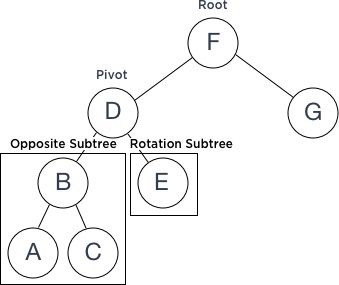
For the rotation we’re using the terminology:
- Root - the parent node of the subtrees that will be rotated;
- Pivot - the node that will become parent (basically will be on the Root’s position) after rotation;
- RotationSubtree - subtree of the Pivot upon the side of rotation
- OppositeSubtree - subtree of the Pivot opposite the side of rotation
Let take an example of balancing the unbalanced tree using Right (clockwise direction) rotation:
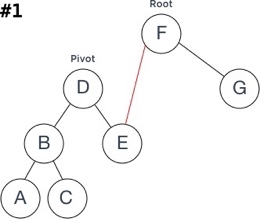
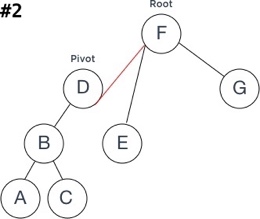
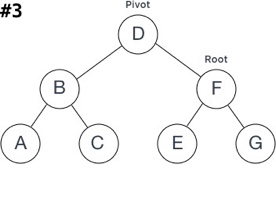
The steps of rotation could be described by following:
- Assign the RotationSubtree as a new OppositeSubtree for the Root;
- Assign the Root as a new RotationSubtree for the Pivot;
- Check the final result
In pseudocode the algorithm above could be written as follows:
Root.OS = Pivot.RS
Pivot.RS = Root
Root = Pivot
This is a constant time operation - O(1) Insertion never needs more than 2 rotations. Removal might require up to log(n) rotations.
The code
Most of the code in AVLTree.swift is just regular binary search tree stuff. You’ll find this in any implementation of a binary search tree. For example, searching the tree is exactly the same. The only things that an AVL tree does slightly differently are inserting and deleting the nodes.
Note: If you’re a bit fuzzy on the regular operations of a binary search tree, I suggest you catch up on those first. It will make the rest of the AVL tree easier to understand.
The interesting bits are in the balance() method which is called after inserting or deleting a node.
See also
AVL tree was the first self-balancing binary tree. These days, the red-black tree seems to be more popular.
Written for Swift Algorithm Club by Mike Taghavi and Matthijs Hollemans