二叉搜索树(BST)
这里有个例子
二叉搜索树是一种特殊的 二叉树 (该树每个父节点最多有两个子节点),在插入和删除后总是保持顺序。
想了解关于树的知识?请先看这里.
“排序”树
这里有一个二叉搜索树的图:
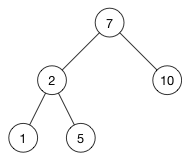
可以看到左边子节点总是比它的父节点小,而右边子节点总是比它的父节点大。这是二叉搜索树的关键特点。
如 2 比 7 小,因此它在左边,而 5 比 2 大,因此它在右边
插入一个新节点
插入新节点时,先与根节点比较,如果较小则走 左 分支,如果较大则走 右 分支。继续如此比较操作,直到我们找到一个空节点可以插入。
比如我们需要插入一个新值 9:
- 从根节点开始(根节点是
7)与新值9做比较, 9 > 7,向右分支下移,这次遇到的节点是10- 因为
9 < 10, 向左下分支移动 - 现在没有值可以进行比较,把
9插入这里
下面是插入 9 后的树:
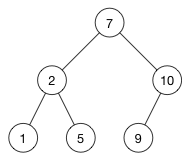
对于新元素只有一个位置可以插入,查找该位置非常快,需要 O(h) 时间, h 为树的高度
注意: 节点 高度 是从此节点到叶子节点的步数。树的总高度是根节点到最低叶子节点的距离。许多二叉搜索树的操作是跟树个高度有关的。
通过遵循这个简单规则 – 小值在左边,大值在右边。我们可以保持树的顺序,所以无论什么时候我们都可以查询这个值是否在树上。
树的查找
为了查找一个值是否在树中,我们采用以下的步骤:
- 如果值小于当前值,取左边树
- 如果值大于当前值,取右边树
- 如果当前值等于当前节点值,就找到了!
就像大部分对树的操作,查找也是不断的递归直到找到节点或者查找结束。
下面是搜索 5 的例子:
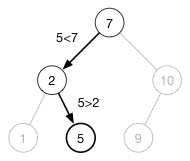
树的搜索是很快的,是 O(h) 时间复杂度。如果是一个平衡很好的树,即使有百万的节点,也不过需要 20 步就能结束查找(和二分搜索的思想很像)。
树的遍历
有时你需要遍历所有的节点,不仅仅只查找单个节点。
共有三种方式来遍历二叉树:
- 中序遍历(或者 深度优先):先访问左子树,然后访问节点本身,最后访问右子树。
- 前序遍历:先访问节点本身,然后访问左子树,最后访问右子树。
- 后序遍历:先访问左子树,然后右子树,最后节点本身。
遍历树也会用到递归。
如果你中序遍历一个二叉搜索树,遍历的结果就像从小到大排列一样。上述例子中的树遍历结果为 1, 2, 5, 7, 9, 10 :
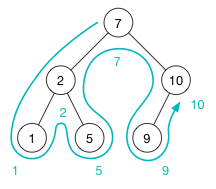
删除节点
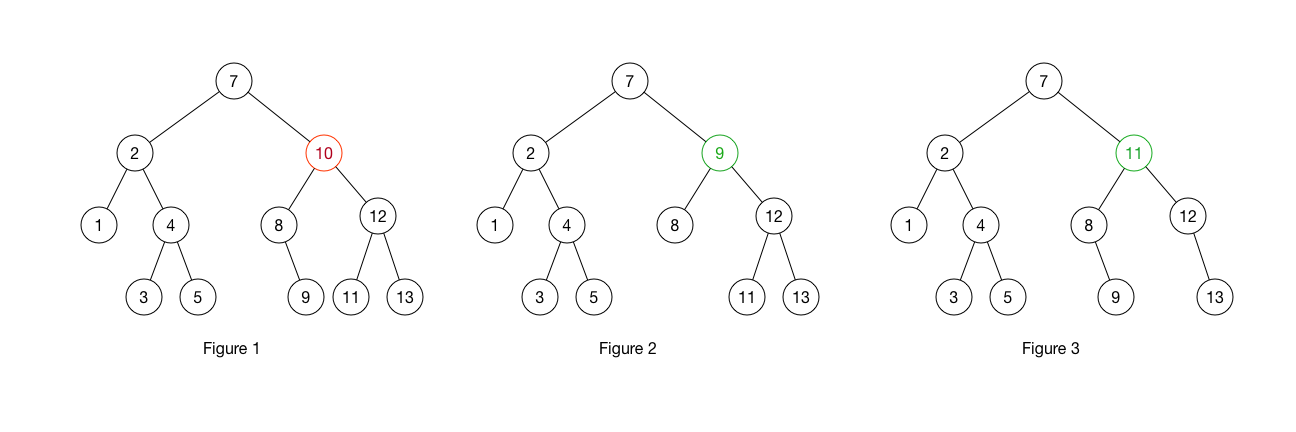
删除节点很简单,删除节点后,把当前的节点替换为它的左子树最大的节点或者右子树最小节点。这样树在删除后还会保持原来的顺序。在下述例子中, 10 被移除, 图2 为用 9 代替, 图3 为用 11 代替。
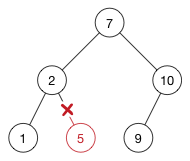
替换节点只会在该节点有子节点的时候才会做,如果没有子节点,你可以直接从它的父节点中移除:
代码 (方法1)
理论介绍到此为止。来看看怎么实现吧,可以使用不同的方式实现, 首先我们先试试建一个基于类的版本,随后我们再用枚举来实现。
这是一个 二叉搜索树 的类:
public class BinarySearchTree<T: Comparable> {
private(set) public var value: T
private(set) public var parent: BinarySearchTree?
private(set) public var left: BinarySearchTree?
private(set) public var right: BinarySearchTree?
public init(value: T) {
self.value = value
}
public var isRoot: Bool {
return parent == nil
}
public var isLeaf: Bool {
return left == nil && right == nil
}
public var isLeftChild: Bool {
return parent?.left === self
}
public var isRightChild: Bool {
return parent?.right === self
}
public var hasLeftChild: Bool {
return left != nil
}
public var hasRightChild: Bool {
return right != nil
}
public var hasAnyChild: Bool {
return hasLeftChild || hasRightChild
}
public var hasBothChildren: Bool {
return hasLeftChild && hasRightChild
}
public var count: Int {
return (left?.count ?? 0) + 1 + (right?.count ?? 0)
}
}
这是一个单节点,它使用了泛型可以存储任意类型数据,它引用了一个 left 和 right 子节点以及 parent 父节点。
来试试:
let tree = BinarySearchTree<Int>(value: 7)
count 是指树上有多少个节点。它不仅仅统计直接连接的子节点,还包含了它的子节点以及子节点的全部后代。如果它是根节点,那么计算的是整个树。初始值为 0。
注意: 因为
left,right和parent是可选值,我们正好可以使用 Swift 的可选链 (?) 以及可选值联合运算符 (??)。 也可以使用if let的方法,但是这样代码更简练。
插入
只有一个的树节点没什么意义,让我们插入一些新的节点:
public func insert(value: T) {
if value < self.value {
if let left = left {
left.insert(value: value)
} else {
left = BinarySearchTree(value: value)
left?.parent = self
}
} else {
if let right = right {
right.insert(value: value)
} else {
right = BinarySearchTree(value: value)
right?.parent = self
}
}
}
类似树的其他操作,插入操作也是递归实现的。我们比较新值与已有节点来决定是放在左子树还是右子树。
如果没有左或右子树在比较了,创建一个 BinarySearchTree 对象并和 parent 建立连接。
注意: 因为整个二叉搜索树必须保持左边是小值,右边是大值的顺序,因此插入一个新元素后必须还是一个正确的二叉树。
插入一些节点吧:
let tree = BinarySearchTree<Int>(value: 7)
tree.insert(2)
tree.insert(5)
tree.insert(10)
tree.insert(9)
tree.insert(1)
注意: 为了后面讲的更清楚,需要随机插入数字,如果排序后再插入它们,树的形状可能会不正确。
创建一个支持数组插入的快捷方法 insert() :
public convenience init(array: [T]) {
precondition(array.count > 0)
self.init(value: array.first!)
for v in array.dropFirst() {
insert(value: v)
}
}
现在简单了:
let tree = BinarySearchTree<Int>(array: [7, 2, 5, 10, 9, 1])
数组中的第一个元素是树的根节点。
Debug输出
在处理一些复杂的数据结构的时候,使用一些可读的 debug 输出非常有用。
extension BinarySearchTree: CustomStringConvertible {
public var description: String {
var s = ""
if let left = left {
s += "(\(left.description)) <- "
}
s += "\(value)"
if let right = right {
s += " -> (\(right.description))"
}
return s
}
}
使用 print(tree) 打印如下:
((1) <- 2 -> (5)) <- 7 -> ((9) <- 10)
根节点在中间,想象一下可以看出其实是一颗这样的树:

你可能好奇如果输入一个重复数据会怎样?答案是总是插在右子树上。试试看!
查找
现在我们树上有一些值了,做什么好呢?当然是做查找啦!查找快速是使用二叉搜索树的主要目的。 :-)
这是 search() 的实现:
public func search(value: T) -> BinarySearchTree? {
if value < self.value {
return left?.search(value)
} else if value > self.value {
return right?.search(value)
} else {
return self // found it!
}
}
逻辑非常明确:从当前节点开始(一般是从根节点开始)比较。如果目标值比当前节点小,继续从左子树查找,如果比当前节点值大,从右子树开始查找。
如果 left 或 right 为 nil,返回 nil 表示没有查到。
注意 在 Swift 中,使用可选链非常方便。
left?.search(value)中left为 nil 的时候会自动返回 nil, 不需要明确的检查。
查找是一个递归的过程,也可以用一个简单的循环代替:
public func search(value: T) -> BinarySearchTree? {
var node: BinarySearchTree? = self
while let n = node {
if value < n.value {
node = n.left
} else if value > n.value {
node = n.right
} else {
return node
}
}
return nil
}
这两种实现是等价的。就个人而言,我更倾向使用循环的方式,人各有志,没关系。 ;-)
测试代码如下:
tree.search(5)
tree.search(2)
tree.search(7)
tree.search(6) // nil
前三行返回相应的 BinaryTreeNode 对象,最后一行返回 nil, 因为没有 6 这个节点。
注意: 如果树中含有重复值,
search()函数会返回最高的节点,这也很合理,因为是从根节点开始查找的。
遍历
还记得遍历树的三种方式吗? 下面就是其实现。
public func traverseInOrder(process: (T) -> Void) {
left?.traverseInOrder(process: process)
process(value)
right?.traverseInOrder(process: process)
}
public func traversePreOrder(process: (T) -> Void) {
process(value)
left?.traversePreOrder(process: process)
right?.traversePreOrder(process: process)
}
public func traversePostOrder(process: (T) -> Void) {
left?.traversePostOrder(process: process)
right?.traversePostOrder(process: process)
process(value)
}
他们功能一模一样,但是输出顺序截然不同。所有的遍历是通过递归实现的。 Swift 的可选链使调用 traverseInOrder () 等函数可以忽略是否有没有左右子树。
从低到高输出树的所有值:
tree.traverseInOrder { value in print(value) }
This prints the following:
1
2
5
7
9
10
你也可以添加 map() 和 filter() 方法。下面是 map 的实现:
public func map(formula: (T) -> T) -> [T] {
var a = [T]()
if let left = left { a += left.map(formula: formula) }
a.append(formula(value))
if let right = right { a += right.map(formula: formula) }
return a
}
每个树上的节点调用 formula 后的结果存入数组中。 map() 是与中序遍历一起完成的。
下面是 map() 一个简单的使用例子:
public func toArray() -> [T] {
return map { $0 }
}
这个函数可以把树的存值变成一个排序后的数组,在 playground 中试一下:
tree.toArray() // [1, 2, 5, 7, 9, 10]
作为练习,你来实现 filter 和 reduce 吧。
删除
先定义一些帮助函数,让代码更加易读:
private func reconnectParentTo(node: BinarySearchTree?) {
if let parent = parent {
if isLeftChild {
parent.left = node
} else {
parent.right = node
}
}
node?.parent = parent
}
这个函数的作用是批量修改树的 parent, left 和 right 指针。可以把当前节点(self)的父节点重新连接另一个子节点。
我们还需要一个函数返回节点的最小值和最大值:
public func minimum() -> BinarySearchTree {
var node = self
while let next = node.left {
node = next
}
return node
}
public func maximum() -> BinarySearchTree {
var node = self
while let next = node.right {
node = next
}
return node
}
剩余代码如下:
@discardableResult public func remove() -> BinarySearchTree? {
let replacement: BinarySearchTree?
//当前节点的代替者要么是左边的最大值,要么是右边的最小值,哪一个都不会为nil
if let right = right {
replacement = right.minimum()
} else if let left = left {
replacement = left.maximum()
} else {
replacement = nil
}
replacement?.remove()
// 把要代替的节点移到当前节点位置
replacement?.right = right
replacement?.left = left
right?.parent = replacement
left?.parent = replacement
reconnectParentTo(node:replacement)
//当前节点不再是树的一部分,因此可以清理删除了
parent = nil
left = nil
right = nil
return replacement
}
深度和高度
某一节点的高度是它到最低叶子节点的距离。我们可以如下计算:
public func height() -> Int {
if isLeaf {
return 0
} else {
return 1 + max(left?.height() ?? 0, right?.height() ?? 0)
}
}
取左右子树的高度作为该节点的高度。递归再一次解决了这个问题。 由于需要查看所有字节,时间复杂度为 O(n) 。
注意: Swift的可选值联合运算符可以减少
left和right的判空处理,你也可以用if let,但是这样代码更简练。
测试:
tree.height() // 2
节点 深度 是指到根节点的距离,代码如下:
public func depth() -> Int {
var node = self
var edges = 0
while let parent = node.parent {
node = parent
edges += 1
}
return edges
}
通过 parent 指针一步一步向上遍历树,直到找到根节点( 根节点的 parent 值为空)。时间复杂度为 O(h) :
if let node9 = tree.search(9) {
node9.depth() // returns 2
}
前驱和后继
二叉搜索树总是 排序 的,但是这不意味着树中连续的数字是相邻的。

只看 7 的左子树是无法找到它的前驱的,因为左子树是 2, 正确的前驱是 5。 后驱也是类似。
predecessor() 函数返回当前节点的前驱
public func predecessor() -> BinarySearchTree<T>? {
if let left = left {
return left.maximum()
} else {
var node = self
while let parent = node.parent {
if parent.value < value { return parent }
node = parent
}
return nil
}
}
有左子树的情况下,前驱就是左子树的最大值。(因为左子树均小于当前节点值,那么左子树最大的值就是最靠近节点的值,译者注)从上图中可以看到 5 是 7 左子树中最大的值。
如果没有左子树,只能一直遍历父节点直到找到比自己小的值。(右子树都不比自己大,左子树没有,最多可能在父节点中,译者注)。想知道 9 的前驱是谁吗?通过这样的方法找到的是 7。
后继 工作方式类似,做个左右对称替换就好了:
public func successor() -> BinarySearchTree<T>? {
if let right = right {
return right.minimum()
} else {
var node = self
while let parent = node.parent {
if parent.value > value { return parent }
node = parent
}
return nil
}
}
这两个方法的时间复杂度为 O(h)
注意: 线索二叉树 变通了一下,把
无用的左右指针重新设计用来直接指向前驱和后继节点。非常有想法!
树是否合法呢?
有一些做法可以破坏树的结构,在非根节点上调用 insert() 方式可能会破坏树的结构。如:
if let node1 = tree.search(1) {
node1.insert(100)
}
根节点是 7, 因此 100 肯定是在右子树上。但是不在根节点上操作而是在一个叶子树上插入新节点, 因此 100 被插入了错误的位置。
导致的问题就是 tree.search(100) 返回 nil。
你可以通过如下方法来判断二叉搜索树是否合法:
public func isBST(minValue minValue: T, maxValue: T) -> Bool {
if value < minValue || value > maxValue { return false }
let leftBST = left?.isBST(minValue: minValue, maxValue: value) ?? true
let rightBST = right?.isBST(minValue: value, maxValue: maxValue) ?? true
return leftBST && rightBST
}
验证方法是左子树值包含的值只会小于当前值,右子树包含色值只会大于当前值。
调用如下:
if let node1 = tree.search(1) {
tree.isBST(minValue: Int.min, maxValue: Int.max) // true
node1.insert(100) // EVIL!!!
tree.search(100) // nil
tree.isBST(minValue: Int.min, maxValue: Int.max) // false
}
代码(方案2)
我们先用类实现了一次,也可以用枚举来实现。
关键的区别就是引用类型和值类型。基于类实现的树更新时是内存的同一个实例,而枚举实现的树是不可改变的,每次插入或者删除操作后会给你一个全新的一个树的拷贝,哪一种更好呢? 这完全取决于你要做什么。
这是我们用枚举实现的二叉搜索树:
public enum BinarySearchTree<T: Comparable> {
case Empty
case Leaf(T)
indirect case Node(BinarySearchTree, T, BinarySearchTree)
}
枚举有三种:
- Empty
表示分支结束(类实现的用nil`) Leaf是一个叶子节点没有子节点Node是一个节点含有一个或者两个子节点。 用indirect修饰,这样它就能包含BinarySearchTree的值。没有indirect无法使用枚举递归。
注意: 二叉树的节点并没有引用它们的父节点。这倒不是大问题,可以用特定的方式来实现。
用递归实现,不同枚举有不同的结果。如下,这是一个实现计算节点数量和高度的代码
public var count: Int {
switch self {
case .Empty: return 0
case .Leaf: return 1
case let .Node(left, _, right): return left.count + 1 + right.count
}
}
public var height: Int {
switch self {
case .Empty: return -1
case .Leaf: return 0
case let .Node(left, _, right): return 1 + max(left.height, right.height)
}
}
插入新节点如下:
public func insert(newValue: T) -> BinarySearchTree {
switch self {
case .Empty:
return .Leaf(newValue)
case .Leaf(let value):
if newValue < value {
return .Node(.Leaf(newValue), value, .Empty)
} else {
return .Node(.Empty, value, .Leaf(newValue))
}
case .Node(let left, let value, let right):
if newValue < value {
return .Node(left.insert(newValue), value, right)
} else {
return .Node(left, value, right.insert(newValue))
}
}
}
在 playground 调用:
var tree = BinarySearchTree.Leaf(7)
tree = tree.insert(2)
tree = tree.insert(5)
tree = tree.insert(10)
tree = tree.insert(9)
tree = tree.insert(1)
注意,每次插入后会得到一个新的树对象。因此需要把新结果赋值给 tree
下面是树最重要的功能-查找:
public func search(x: T) -> BinarySearchTree? {
switch self {
case .Empty:
return nil
case .Leaf(let y):
return (x == y) ? self : nil
case let .Node(left, y, right):
if x < y {
return left.search(x)
} else if y < x {
return right.search(x)
} else {
return self
}
}
}
大多数的函数有相同的代码结构。
调用:
tree.search(10)
tree.search(1)
tree.search(11) // nil
使用如下的方法做 Debug
extension BinarySearchTree: CustomDebugStringConvertible {
public var debugDescription: String {
switch self {
case .Empty: return "."
case .Leaf(let value): return "\(value)"
case .Node(let left, let value, let right):
return "(\(left.debugDescription) <- \(value) -> \(right.debugDescription))"
}
}
}
打印如下:
((1 <- 2 -> 5) <- 7 -> (9 <- 10 -> .)) 根节点在中点,点 代表是没有子节点。
树如果不平衡了..
平衡 二叉搜索树左右子树有相同的节点。在这种情况下是理想状态,树的高度是 log(n), n 为节点的个数。
当一个分支明显的比其他长时查找会变的很慢。在最坏的情况下,树的高度变成 n, 这样不再是二叉搜索树,更像是 链表。时间复杂度变成 O(n), 性能会差很多,非常糟糕。
一种方法是随机插入使得二叉搜索树保持平衡。一般情况下应该能保持树的平衡,但是这样无法保证,实际也确实如此。
另一种方式是使用 自平衡 的二叉搜索树。这种数据结构能在插入或删除后调整树的平衡。如 AVL树 和 红黑树。
更多
Binary Search Tree on Wikipedia
作者 Nicolas Ameghino 、 Matthijs Hollemans,译者:KeithMorning