Egg Drop

The egg drop problem is an interview question popularized by Google. The premise is simple; You’re given a task to evaluate the shatter resistance of unknown objects by dropping them at a certain height. For simplicity, you test this by going inside a multi-story building and performing tests by dropping the objects out the window and onto the ground:

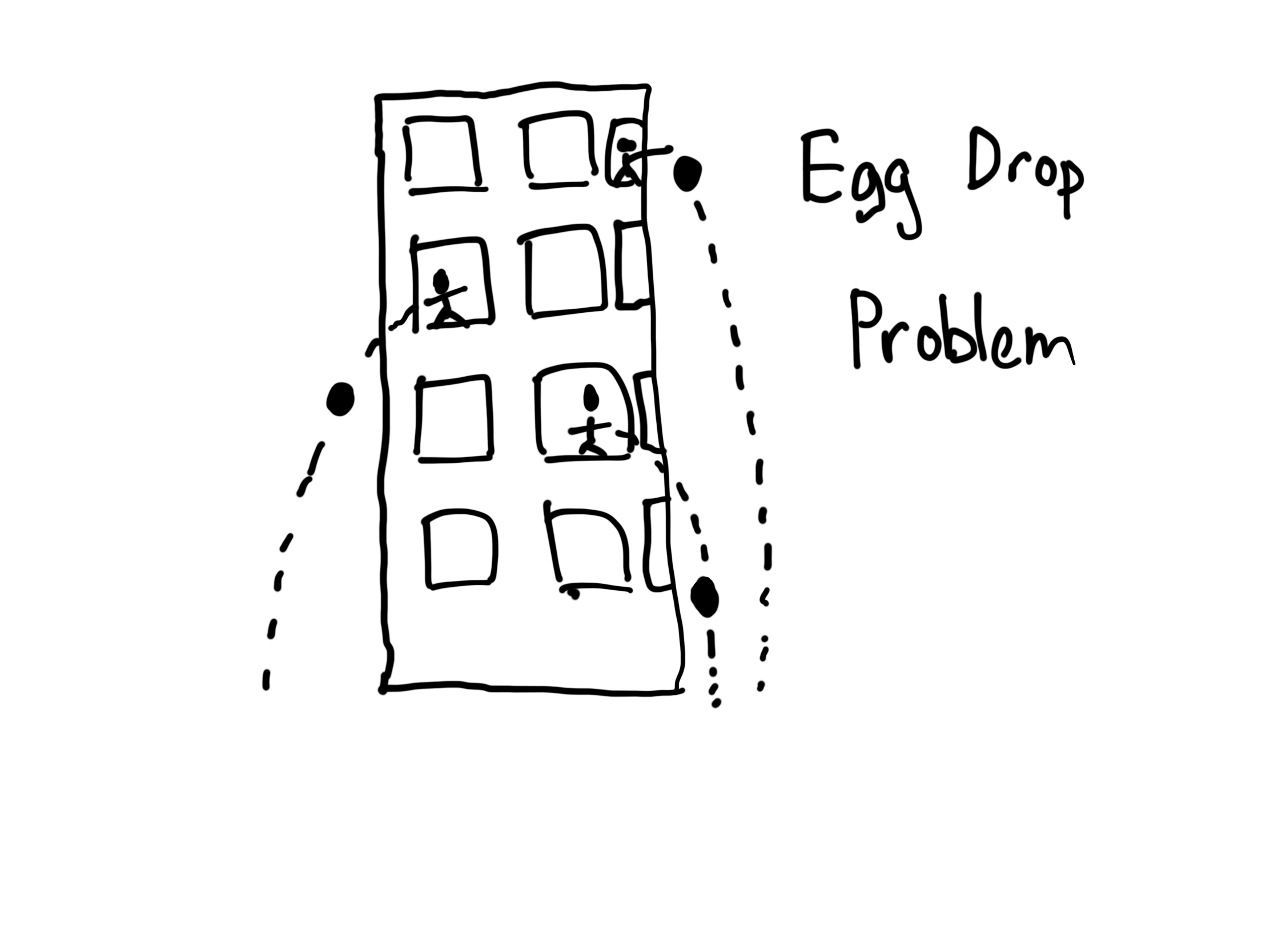
Your goal is to find out the minimum height that causes the object to shatter. Consider the trivial case you’re given 1 object to obtain the results with. Since you’ve only got one sample for testing, you need to play it safe by performing drop tests starting with the bottom floor and working your way up:

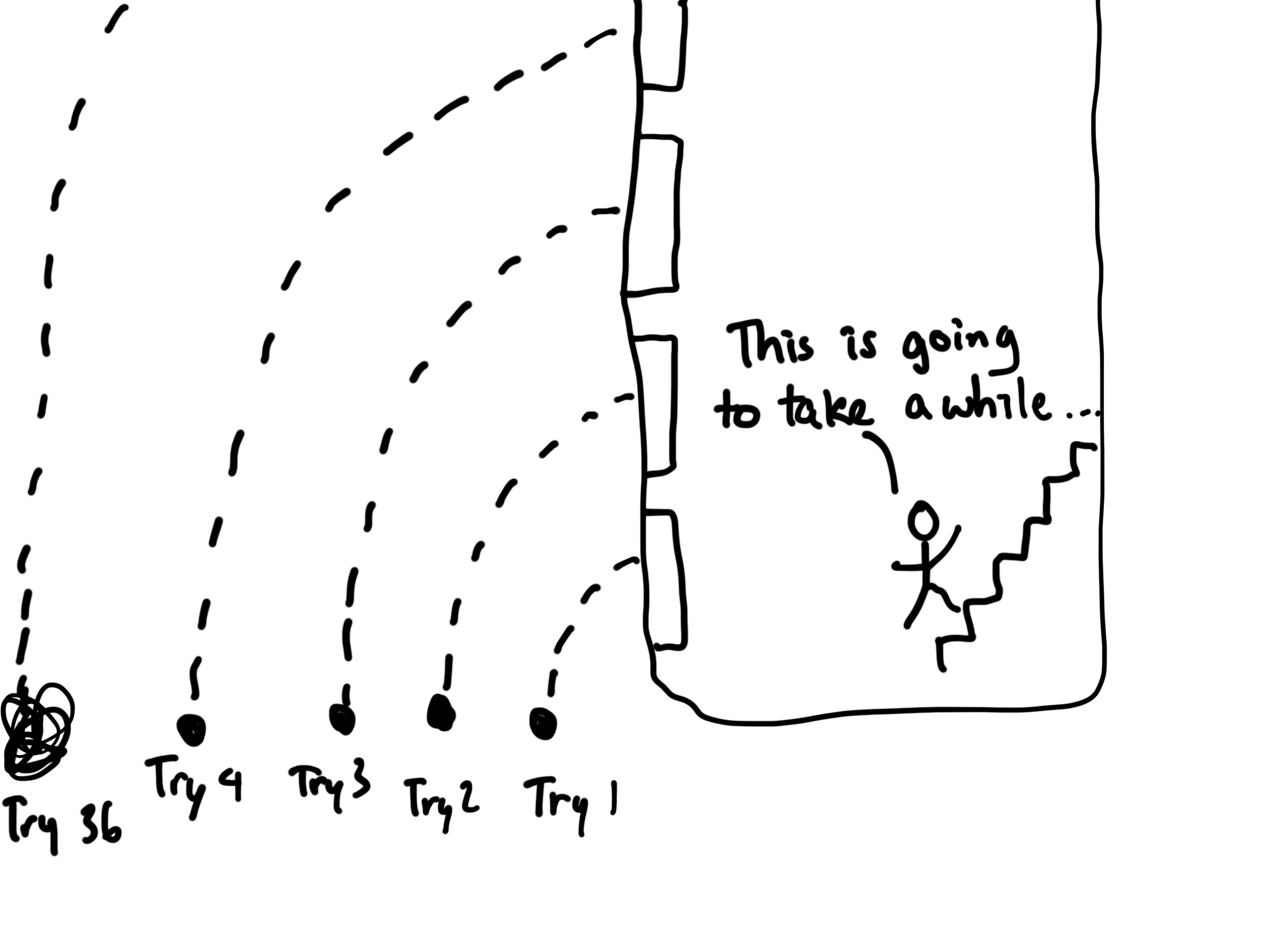
If the object is incredibly resilient, and you may need to do the testing on the world’s tallest building - the Burj Khalifa. With 163 floors, that’s a lot of climbing. Let’s assume you complain, and your employer hears your plight. You are now given several samples to work with. How can you make use of these extra samples to expedite your testing process? The problem for this situation is popularized as the egg drop problem.

Description

You’re in a building with m floors and you are given n eggs. What is the minimum number of attempts it will take to find out the floor that breaks the egg?

For convenience, here are a few rules to keep in mind:

• An egg that survives a fall can be used again.
• A broken egg must be discarded.
• The effect of a fall is the same for all eggs.
• If an egg breaks, then it would break if dropped from a higher floor.
• If an egg survives, then it would survive a shorter fall.

Solution

• eggNumber -> Number of eggs at the moment
• floorNumber -> Floor number at the moment
• visitingFloor -> Floor being visited at the moment
• attempts -> Minimum number of attempts it will take to find out from which floor egg will break

We store all the solutions in a 2D array. Where rows represents number of eggs and columns represent number of floors.

First, we set base cases: 1) If there’s only one egg, it takes as many attempts as number of floors 2) If there are two eggs and one floor, it takes one attempt

for var floorNumber in (0..<(numberOfFloors+1)){
eggFloor[1][floorNumber] = floorNumber      //base case 1: if there's only one egg, it takes 'numberOfFloors' attempts
}

eggFloor[2][1] = 1 //base case 2: if there are two eggs and one floor, it takes one attempt

When we drop an egg from a floor ‘floorNumber’, there can be two cases (1) The egg breaks (2) The egg doesn’t break.

1) If the egg breaks after dropping from ‘visitingFloorth’ floor, then we only need to check for floors lower than ‘visitingFloor’ with remaining eggs; so the problem reduces to ‘visitingFloor’-1 floors and ‘eggNumber’-1 eggs. 2) If the egg doesn’t break after dropping from the ‘visitingFloorth’ floor, then we only need to check for floors higher than ‘visitingFloor’; so the problem reduces to floors-‘visitingFloor’ floors and ‘eggNumber’ eggs.

Since we need to minimize the number of trials in worst case, we take the maximum of two cases. We consider the max of above two cases for every floor and choose the floor which yields minimum number of trials.

We find the answer based on the base cases and previously found answers as follows.

attempts = 1 + max(eggFloor[eggNumber-1][floors-1], eggFloor[eggNumber][floorNumber-floors])//we add one taking into account the attempt we're taking at the moment

if attempts < eggFloor[eggNumber][floorNumber]{ //finding the min
    eggFloor[eggNumber][floorNumber] = attempts;
}

Example

Let’s assume we have 2 eggs and 2 floors. 1) We drop one egg from the first floor. If it breaks, then we get the answer. If it doesn’t we’ll have 2 eggs and 1 floors to work with. attempts = 1 + maximum of 0(got the answer) and eggFloor[2][1] (base case 2 which gives us 1) attempts = 1 + 1 = 2 2) We drop one egg from the second floor. If it breaks, we’ll have 1 egg and 1 floors to work with. If it doesn’t, we’ll get the answer. attempts = 1 + maximum of eggFloor[1]1 and 0(got the answer) attempts = 1 + 1 = 2 3) Finding the minimum of 2 and 2 gives us 2, so the answer is 2. 2 is the minimum number of attempts it will take to find out from which floor egg will break.

Written for the Swift Algorithm Club by Arkalyk Akash. Revisions and additions by Kelvin Lau