Huffman Coding
The idea: To encode objects that occur often with a smaller number of bits than objects that occur less frequently.
Although any type of objects can be encoded with this scheme, it is common to compress a stream of bytes. Suppose you have the following text, where each character is one byte:
so much words wow many compression
If you count how often each byte appears, you can see some bytes occur more than others:
space: 5 u: 1
o: 5 h: 1
s: 4 d: 1
m: 3 a: 1
w: 3 y: 1
c: 2 p: 1
r: 2 e: 1
n: 2 i: 1
We can assign bit strings to each of these bytes. The more common a byte is, the fewer bits we assign to it. We might get something like this:
space: 5 010 u: 1 11001
o: 5 000 h: 1 10001
s: 4 101 d: 1 11010
m: 3 111 a: 1 11011
w: 3 0010 y: 1 01111
c: 2 0011 p: 1 11000
r: 2 1001 e: 1 01110
n: 2 0110 i: 1 10000
Now if we replace the original bytes with these bit strings, the compressed output becomes:
101 000 010 111 11001 0011 10001 010 0010 000 1001 11010 101
s o _ m u c h _ w o r d s
010 0010 000 0010 010 111 11011 0110 01111 010 0011 000 111
_ w o w _ m a n y _ c o m
11000 1001 01110 101 101 10000 000 0110 0
p r e s s i o n
The extra 0-bit at the end is there to make a full number of bytes. We were able to compress the original 34 bytes into merely 16 bytes, a space savings of over 50%!
To be able to decode these bits, we need to have the original frequency table. That table needs to be transmitted or saved along with the compressed data. Otherwise, the decoder does not know how to interpret the bits. Because of the overhead of this frequency table (about 1 kilobyte), it is not beneficial to use Huffman encoding on small inputs.
How it works
When compressing a stream of bytes, the algorithm first creates a frequency table that counts how often each byte occurs. Based on this table, the algorithm creates a binary tree that describes the bit strings for each of the input bytes.
For our example, the tree looks like this:
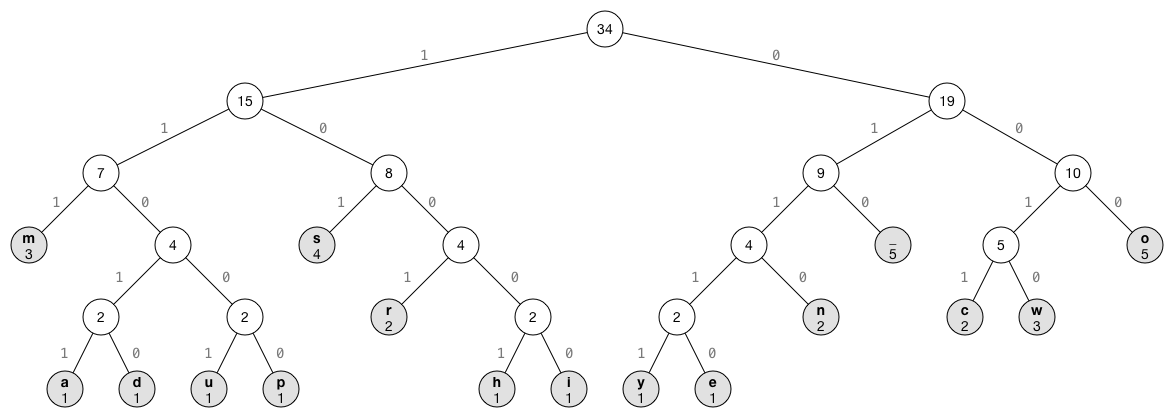
Note that the tree has 16 leaf nodes (the grey ones), one for each byte value from the input. Each leaf node also shows the count of how often it occurs. The other nodes are “intermediate” nodes. The number shown in these nodes is the sum of the counts of their child nodes. The count of the root node is therefore the total number of bytes in the input.
The edges between the nodes are either “1” or “0”. These correspond to the bit-encodings of the leaf nodes. Notice how each left branch is always 1 and each right branch is always 0.
Compression is then a matter of looping through the input bytes and for each byte traversing the tree from the root node to that byte’s leaf node. Every time we take a left branch, we emit a 1-bit. When we take a right branch, we emit a 0-bit.
For example, to go from the root node to c, we go right (0), right again (0), left (1), and left again (1). This gives the Huffman code as 0011 for c.
Decompression works in exactly the opposite way. It reads the compressed bits one-by-one and traverses the tree until it reaches to a leaf node. The value of that leaf node is the uncompressed byte. For example, if the bits are 11010, we start at the root and go left, left again, right, left, and a final right to end up at d.
The code
Before we get to the actual Huffman coding scheme, it is useful to have some helper code that can write individual bits to an NSData object. The smallest piece of data that NSData understands is the byte, but we are dealing in bits, so we need to translate between the two.
public class BitWriter {
public var data = NSMutableData()
var outByte: UInt8 = 0
var outCount = 0
public func writeBit(bit: Bool) {
if outCount == 8 {
data.append(&outByte, length: 1)
outCount = 0
}
outByte = (outByte << 1) | (bit ? 1 : 0)
outCount += 1
}
public func flush() {
if outCount > 0 {
if outCount < 8 {
let diff = UInt8(8 - outCount)
outByte <<= diff
}
data.append(&outByte, length: 1)
}
}
}
To add a bit to the NSData, you can call writeBit(). This helper object stuffs each new bit into the outByte variable. Once you have written 8 bits, outByte gets added to the NSData object for real.
The flush() method is used for outputting the very last byte. There is no guarantee that the number of compressed bits is a nice round multiple of 8, in which case there may be some spare bits at the end. If so, flush() adds a few 0-bits to make sure that we write a full byte.
Here is a similar helper object for reading individual bits from NSData:
public class BitReader {
var ptr: UnsafePointer<UInt8>
var inByte: UInt8 = 0
var inCount = 8
public init(data: NSData) {
ptr = data.bytes.assumingMemoryBound(to: UInt8.self)
}
public func readBit() -> Bool {
if inCount == 8 {
inByte = ptr.pointee // load the next byte
inCount = 0
ptr = ptr.successor()
}
let bit = inByte & 0x80 // read the next bit
inByte <<= 1
inCount += 1
return bit == 0 ? false : true
}
}
By using this helper object, we can read one whole byte from the NSData object and put it in inByte. Then, readBit() returns the individual bits from that byte. Once readBit() has been called 8 times, we read the next byte from the NSData.
Note: If you are unfamiliar with this type of bit manipulation, just know that these two helper objects make it simple for us to write and read bits.
The frequency table
The first step in the Huffman compression is to read the entire input stream and build a frequency table. This table contains a list of all 256 possible byte values and shows how often each of these bytes occurs in the input data.
We could store this frequency information in a dictionary or an array, but since we need to build a tree, we might store the frequency table as the leaves of the tree.
Here are the definitions we need:
class Huffman {
typealias NodeIndex = Int
struct Node {
var count = 0
var index: NodeIndex = -1
var parent: NodeIndex = -1
var left: NodeIndex = -1
var right: NodeIndex = -1
}
var tree = [Node](repeating: Node(), count: 256)
var root: NodeIndex = -1
}
The tree structure is stored in the tree array and will be made up of Node objects. Since this is a binary tree, each node needs two children, left and right, and a reference back to its parent node. Unlike a typical binary tree, these nodes do not use pointers to refer to each other but use simple integer indices in the tree array. (We also store the array index of the node itself; the reason for this will become clear later.)
Note that the tree currently has room for 256 entries. These are for the leaf nodes because there are 256 possible byte values. Of course, not all of those may end up being used, depending on the input data. Later, we will add more nodes as we build up the actual tree. For the moment, there is not a tree yet. It includes 256 separate leaf nodes with no connections between them. All the node counts are 0.
We use the following method to count how often each byte occurs in the input data:
fileprivate func countByteFrequency(inData data: NSData) {
var ptr = data.bytes.assumingMemoryBound(to: UInt8.self)
for _ in 0..<data.length {
let i = Int(ptr.pointee)
tree[i].count += 1
tree[i].index = i
ptr = ptr.successor()
}
}
This steps through the NSData object from beginning to end and for each byte increments the count of the corresponding leaf node. After countByteFrequency() completes, the first 256 Node objects in the tree array represent the frequency table.
To decompress a Huffman-encoded block of data, we need to have the original frequency table. If we were writing the compressed data to a file, then somewhere in the file we should include the frequency table.
We could dump the first 256 elements from the tree array, but that is not efficient. Not all of these 256 elements will be used, and we do not need to serialize the parent, right, and left pointers. All we need is the frequency information and not the entire tree.
Instead, we will add a method to export the frequency table without all the pieces we do not need:
struct Freq {
var byte: UInt8 = 0
var count = 0
}
func frequencyTable() -> [Freq] {
var a = [Freq]()
for i in 0..<256 where tree[i].count > 0 {
a.append(Freq(byte: UInt8(i), count: tree[i].count))
}
return a
}
The frequencyTable() method looks at those first 256 nodes from the tree but keeps only those that are used, without the parent, left, and right pointers. It returns an array of Freq objects. You have to serialize this array along with the compressed data, so that it can be properly decompressed later.
The tree
As a reminder, there is the compression tree for the example:

The leaf nodes represent the actual bytes that are present in the input data. The intermediary nodes connect the leaves in such a way that the path from the root to a frequently-used byte value is shorter than the path to a less common byte value. As you can see, m, s, space, and o are the most common letters in our input data and the highest up in the tree.
To build the tree, we do the following:
- Find the two nodes with the smallest counts that do not have a parent node yet.
- Create a new parent node that links these two nodes together.
- This repeats over and over until only one node with no parent remains. This becomes the root node of the tree.
This is an ideal place to use a priority queue. A priority queue is a data structure that is optimized, so that finding the minimum value is always fast. Here, we repeatedly need to find the node with the smallest count.
The function buildTree() then becomes:
fileprivate func buildTree() {
var queue = PriorityQueue<Node>(sort: { $0.count < $1.count })
for node in tree where node.count > 0 {
queue.enqueue(node) // 1
}
while queue.count > 1 {
let node1 = queue.dequeue()! // 2
let node2 = queue.dequeue()!
var parentNode = Node() // 3
parentNode.count = node1.count + node2.count
parentNode.left = node1.index
parentNode.right = node2.index
parentNode.index = tree.count
tree.append(parentNode)
tree[node1.index].parent = parentNode.index // 4
tree[node2.index].parent = parentNode.index
queue.enqueue(parentNode) // 5
}
let rootNode = queue.dequeue()! // 6
root = rootNode.index
}
Here is how it works step-by-step:
-
Create a priority queue and enqueue all the leaf nodes that have at least a count of 1. (If the count is 0, then this byte value did not appear in the input data.) The
PriorityQueueobject sorts the nodes by their count, so that the node with the lowest count is always the first one that gets dequeued. -
While there are at least two nodes left in the queue, remove the two nodes that are at the front of the queue. Since this is a min-priority queue, this gives us the two nodes with the smallest counts that do not have a parent node yet.
-
Create a new intermediate node that connects
node1andnode2. The count of this new node is the sum of the counts ofnode1andnode2. Because the nodes are connected using array indices instead of real pointers, we usenode1.indexandnode2.indexto find these nodes in thetreearray. (This is why aNodeneeds to know its own index.) -
Link the two nodes into their new parent node. Now this new intermediate node has become part of the tree.
-
Put the new intermediate node back into the queue. At this point we are done with
node1andnode2, but theparentNodestill needs to be connected to other nodes in the tree. -
Repeat steps 2-5 until there is only one node left in the queue. This becomes the root node of the tree, and we are done.
The animation shows what the process looks like:
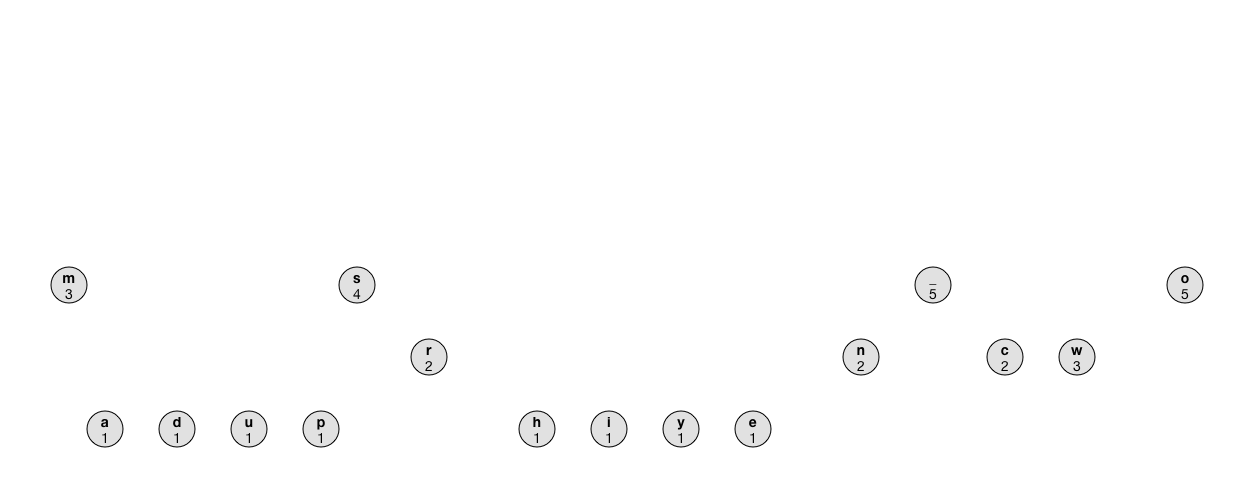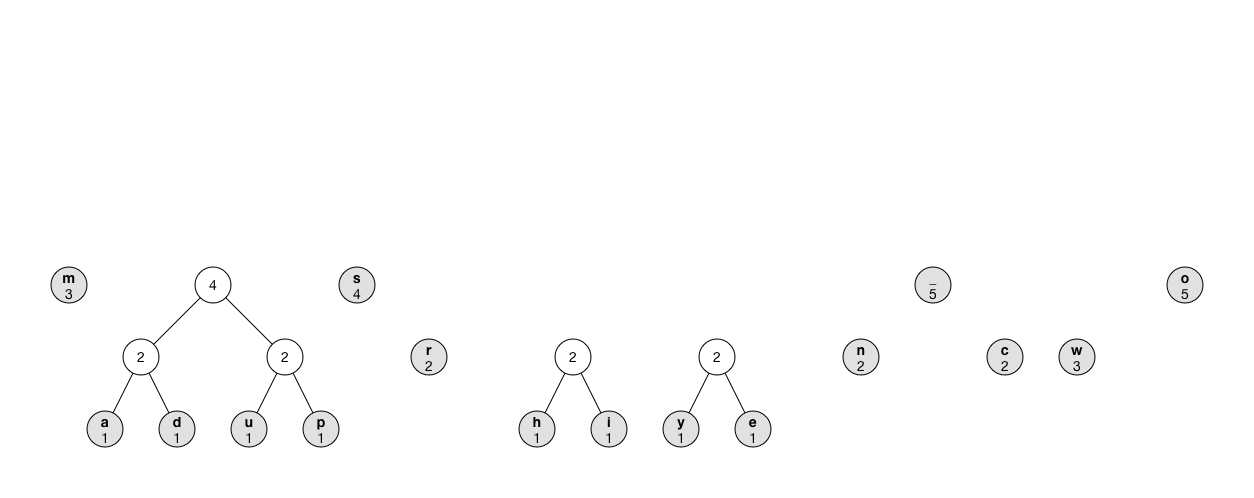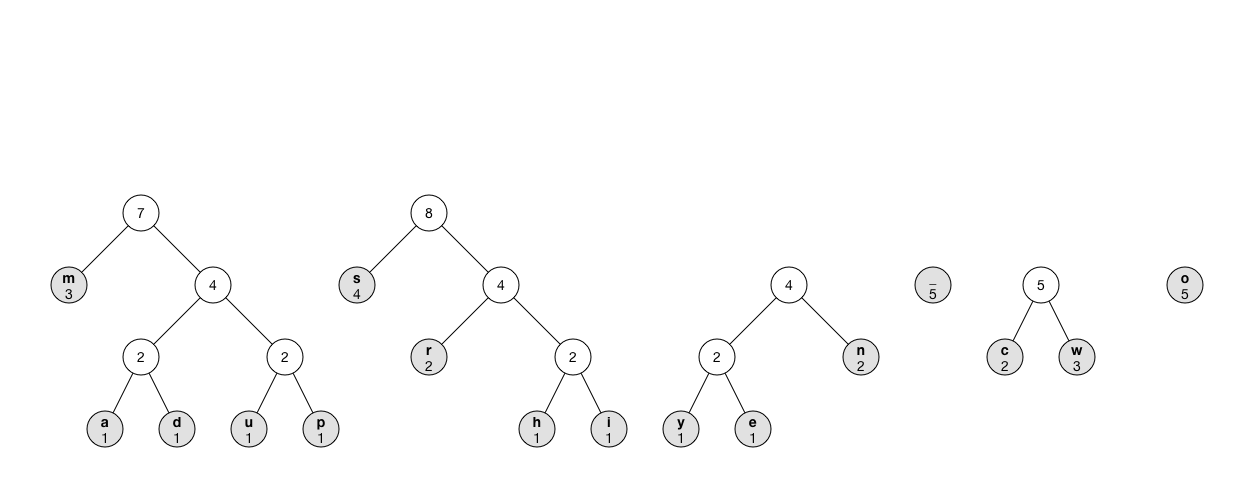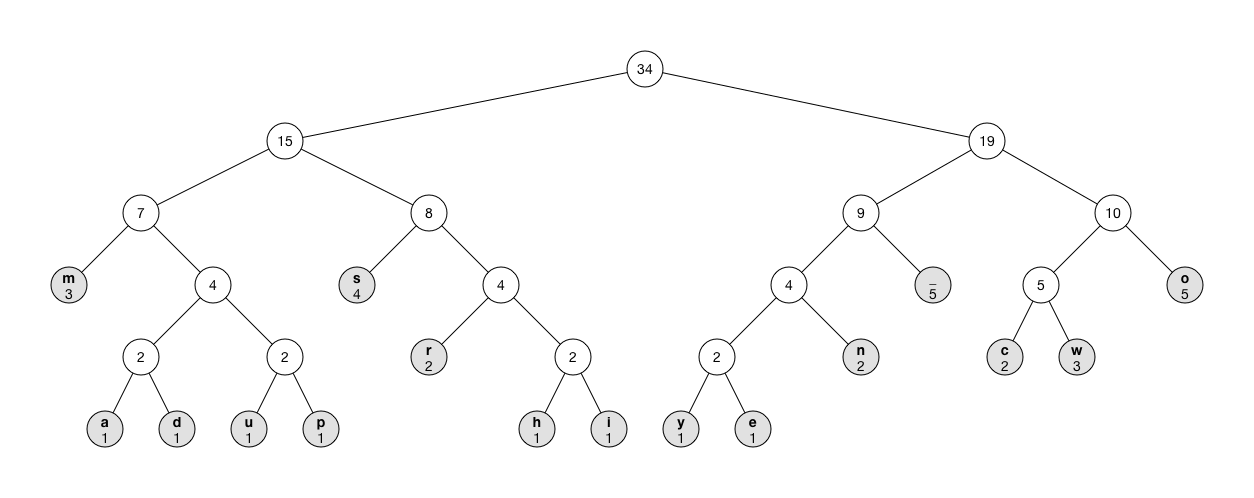
Note: Instead of using a priority queue, you can repeatedly iterate through the
treearray to find the next two smallest nodes, but that makes the compressor slow as O(n^2). Using the priority queue, the running time is only O(n log n) where n is the number of nodes.
Fun fact: Due to the nature of binary trees, if we have x leaf nodes we can at most add x - 1 additional nodes to the tree. Given that at most there will be 256 leaf nodes, the tree will never contain more than 511 nodes total.
Compression
Now that we know how to build the compression tree from the frequency table, we can use it to compress the contents of an NSData object. Here is the code:
public func compressData(data: NSData) -> NSData {
countByteFrequency(inData: data)
buildTree()
let writer = BitWriter()
var ptr = data.bytes.assumingMemoryBound(to: UInt8.self)
for _ in 0..<data.length {
let c = ptr.pointee
let i = Int(c)
traverseTree(writer: writer, nodeIndex: i, childIndex: -1)
ptr = ptr.successor()
}
writer.flush()
return writer.data
}
This first calls countByteFrequency() to build the frequency table and then calls buildTree() to put together the compression tree. It also creates a BitWriter object for writing individual bits.
Then, it loops through the entire input and calls traverseTree()for each byte. This method will step through the tree nodes and for each node write a 1 or 0 bit. Finally, we return the BitWriter’s data object.
Note: Compression always requires two passes through the entire input data: first to build the frequency table, and second to convert the bytes to their compressed bit sequences.
The interesting stuff happens in traverseTree(). This is a recursive method:
private func traverseTree(writer: BitWriter, nodeIndex h: Int, childIndex child: Int) {
if tree[h].parent != -1 {
traverseTree(writer: writer, nodeIndex: tree[h].parent, childIndex: h)
}
if child != -1 {
if child == tree[h].left {
writer.writeBit(bit: true)
} else if child == tree[h].right {
writer.writeBit(bit: false)
}
}
}
When we call this method from compressData(), the nodeIndex parameter is the array index of the leaf node for the byte that we need to encode. This method recursively walks the tree from a leaf node up to the root and then back again.
As we are going back from the root to the leaf node, we write a 1 bit or a 0 bit for every node we encounter. If a child is the left node, we emit a 1; if it is the right node, we emit a 0.
In a picture:
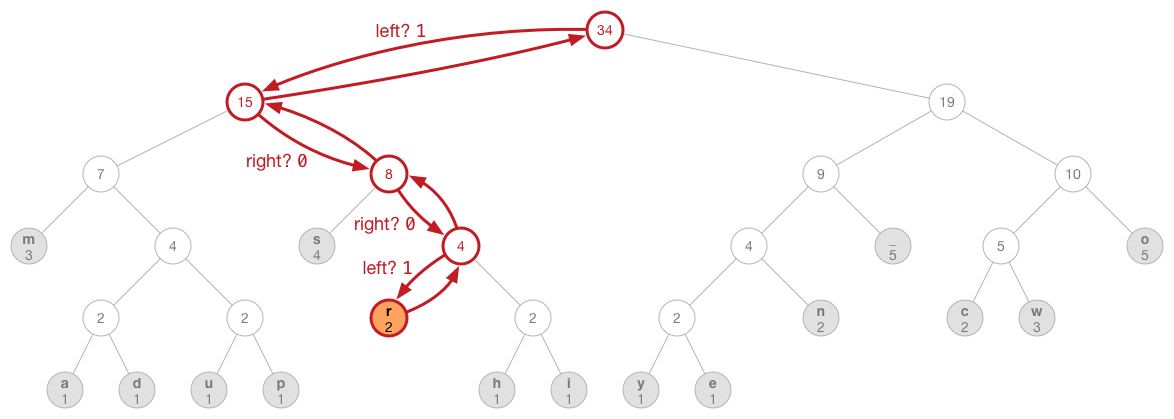
Even though the illustration of the tree shows a 0 or 1 for each edge between the nodes, the bit values 0 and 1 are not actually stored in the tree! The rule is that we write a 1 bit if we take the left branch and a 0 bit if we take the right branch, so just knowing the direction we are going in is enough to determine what bit value to write.
You use the compressData() method as follows:
let s1 = "so much words wow many compression"
if let originalData = s1.dataUsingEncoding(NSUTF8StringEncoding) {
let huffman1 = Huffman()
let compressedData = huffman1.compressData(originalData)
print(compressedData.length)
}
Decompression
Decompression is the compression in reverse. However, the compressed bits are useless without the frequency table. As mentioned, the frequencyTable() method returns an array of Freq objects. If we were saving the compressed data into a file or sending it across the network, we’d also save that [Freq] array along with it.
We first need some way to turn the [Freq] array back into a compression tree:
fileprivate func restoreTree(fromTable frequencyTable: [Freq]) {
for freq in frequencyTable {
let i = Int(freq.byte)
tree[i].count = freq.count
tree[i].index = i
}
buildTree()
}
We convert the Freq objects into leaf nodes and then call buildTree() to do the rest.
Here is the code for decompressData(), which takes an NSData object with Huffman-encoded bits and a frequency table, and it returns the original data:
func decompressData(data: NSData, frequencyTable: [Freq]) -> NSData {
restoreTree(fromTable: frequencyTable)
let reader = BitReader(data: data)
let outData = NSMutableData()
let byteCount = tree[root].count
var i = 0
while i < byteCount {
var b = findLeafNode(reader: reader, nodeIndex: root)
outData.append(&b, length: 1)
i += 1
}
return outData
}
This also uses a helper method to traverse the tree:
private func findLeafNode(reader reader: BitReader, nodeIndex: Int) -> UInt8 {
var h = nodeIndex
while tree[h].right != -1 {
if reader.readBit() {
h = tree[h].left
} else {
h = tree[h].right
}
}
return UInt8(h)
}
findLeafNode() walks the tree from the root down to the leaf node given by nodeIndex. At each intermediate node, we read a new bit and then step to the left (bit is 1) or the right (bit is 0). When we get to the leaf node, we simply return its index, which is equal to the original byte value.
In a picture:
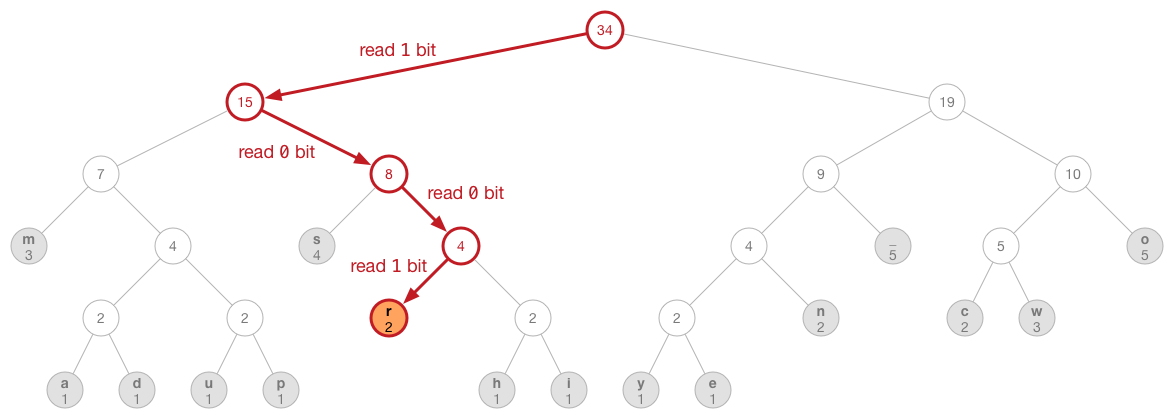
Here is how we use the decompression method:
let frequencyTable = huffman1.frequencyTable()
let huffman2 = Huffman()
let decompressedData = huffman2.decompressData(compressedData, frequencyTable: frequencyTable)
let s2 = String(data: decompressedData, encoding: NSUTF8StringEncoding)!
First we get the frequency table from somewhere (in this case the Huffman object we used to encode the data) and then call decompressData(). The string that results should be equal to the one we compressed in the first place.
we can see how this works in more detail in the Playground.
See also
The code is loosely based on Al Stevens’ C Programming column from Dr.Dobb’s Magazine, February 1991 and October 1992.
Written for Swift Algorithm Club by Matthijs Hollemans