Minimum Spanning Tree (Weighted Graph)

This topic has been tutorialized here

A minimum spanning tree (MST) of a connected undirected weighted graph has a subset of the edges from the original graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. There can be more than one MSTs of a graph.

There are two popular algorithms to calculate MST of a graph - Kruskal’s algorithm and Prim’s algorithm. Both algorithms have a total time complexity of O(ElogE) where E is the number of edges from the original graph.

Kruskal’s Algorithm

Sort the edges base on weight. Greedily select the smallest one each time and add into the MST as long as it doesn’t form a cycle. Kruskal’s algoritm uses Union Find data structure to check whether any additional edge causes a cycle. The logic is to put all connected vertices into the same set (in Union Find’s concept). If the two vertices from a new edge do not belong to the same set, then it’s safe to add that edge into the MST.

The following graph demonstrates the steps:

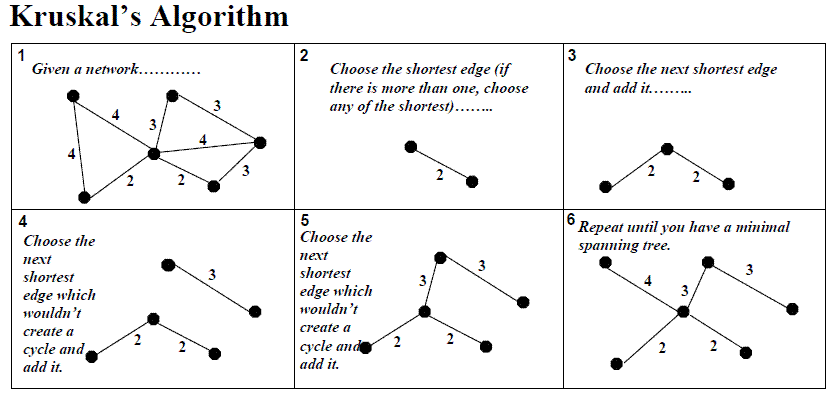
Preparation

// Initialize the values to be returned and Union Find data structure.
var cost: Int = 0
var tree = Graph<T>()
var unionFind = UnionFind<T>()
for vertex in graph.vertices {

// Initially all vertices are disconnected.
// Each of them belongs to it's individual set.
  unionFind.addSetWith(vertex)
}

Sort the edges

let sortedEdgeListByWeight = graph.edgeList.sorted(by: { $0.weight < $1.weight })

Take one edge at a time and try to insert it into the MST.

for edge in sortedEdgeListByWeight {
  let v1 = edge.vertex1
  let v2 = edge.vertex2 
  
  // Same set means the two vertices of this edge were already connected in the MST.
  // Adding this one will cause a cycle.
  if !unionFind.inSameSet(v1, and: v2) {
    // Add the edge into the MST and update the final cost.
    cost += edge.weight
    tree.addEdge(edge)
    
    // Put the two vertices into the same set.
    unionFind.unionSetsContaining(v1, and: v2)
  }
}

Prim’s Algorithm

Prim’s algorithm doesn’t pre-sort all edges. Instead, it uses a Priority Queue to maintain a running sorted next-possile vertices. Starting from one vertex, loop through all unvisited neighbours and enqueue a pair of values for each neighbour - the vertex and the weight of edge connecting current vertex to the neighbour. Each time it greedily select the top of the priority queue (the one with least weight value) and add the edge into the final MST if the enqueued neighbour hasn’t been already visited.

The following graph demonstrates the steps:

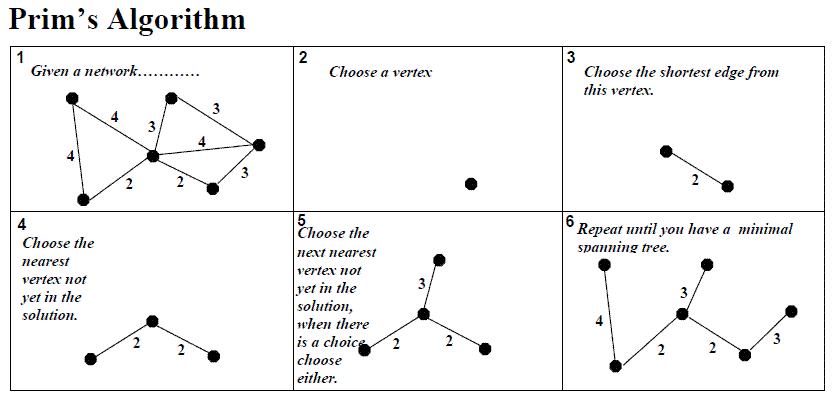
Preparation

// Initialize the values to be returned and Priority Queue data structure.
var cost: Int = 0
var tree = Graph<T>()
var visited = Set<T>()

// In addition to the (neighbour vertex, weight) pair, parent is added for the purpose of printing out the MST later.
// parent is basically current vertex. aka. the previous vertex before neigbour vertex gets visited.
var priorityQueue = PriorityQueue<(vertex: T, weight: Int, parent: T?)>(sort: { $0.weight < $1.weight })

Start from any vertex

priorityQueue.enqueue((vertex: graph.vertices.first!, weight: 0, parent: nil))

// Take from the top of the priority queue ensures getting the least weight edge.
while let head = priorityQueue.dequeue() {
  let vertex = head.vertex
  if visited.contains(vertex) {
    continue
  }

  // If the vertex hasn't been visited before, its edge (parent-vertex) is selected for MST.
  visited.insert(vertex)
  cost += head.weight
  if let prev = head.parent { // The first vertex doesn't have a parent.
    tree.addEdge(vertex1: prev, vertex2: vertex, weight: head.weight)
  }

  // Add all unvisted neighbours into the priority queue.
  if let neighbours = graph.adjList[vertex] {
    for neighbour in neighbours {
      let nextVertex = neighbour.vertex
      if !visited.contains(nextVertex) {
        priorityQueue.enqueue((vertex: nextVertex, weight: neighbour.weight, parent: vertex))
      }
    }
  }
}