Quicksort
Goal: Sort an array from low to high (or high to low).
Quicksort is one of the most famous algorithms in history. It was invented way back in 1959 by Tony Hoare, at a time when recursion was still a fairly nebulous concept.
Here’s an implementation in Swift that should be easy to understand:
func quicksort<T: Comparable>(_ a: [T]) -> [T] {
guard a.count > 1 else { return a }
let pivot = a[a.count/2]
let less = a.filter { $0 < pivot }
let equal = a.filter { $0 == pivot }
let greater = a.filter { $0 > pivot }
return quicksort(less) + equal + quicksort(greater)
}
Put this code in a playground and test it like so:
let list = [ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
quicksort(list)
Here’s how it works. When given an array, quicksort() splits it up into three parts based on a “pivot” variable. Here, the pivot is taken to be the element in the middle of the array (later on you’ll see other ways to choose the pivot).
All the elements less than the pivot go into a new array called less. All the elements equal to the pivot go into the equal array. And you guessed it, all elements greater than the pivot go into the third array, greater. This is why the generic type T must be Comparable, so we can compare the elements with <, ==, and >.
Once we have these three arrays, quicksort() recursively sorts the less array and the greater array, then glues those sorted subarrays back together with the equal array to get the final result.
An example
Let’s walk through the example. The array is initially:
[ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
First, we pick the pivot element. That is 8 because it’s in the middle of the array. Now we split the array into the less, equal, and greater parts:
less: [ 0, 3, 2, 1, 5, -1 ]
equal: [ 8, 8 ]
greater: [ 10, 9, 14, 27, 26 ]
This is a good split because less and greater roughly contain the same number of elements. So we’ve picked a good pivot that chopped the array right down the middle.
Note that the less and greater arrays aren’t sorted yet, so we call quicksort() again to sort those two subarrays. That does the exact same thing: pick a pivot and split the subarray into three even smaller parts.
Let’s just take a look at the less array:
[ 0, 3, 2, 1, 5, -1 ]
The pivot element is the one in the middle, 1. (You could also have picked 2, it doesn’t matter.) Again, we create three subarrays around the pivot:
less: [ 0, -1 ]
equal: [ 1 ]
greater: [ 3, 2, 5 ]
We’re not done yet and quicksort() again is called recursively on the less and greater arrays. Let’s look at less again:
[ 0, -1 ]
As pivot we pick -1. Now the subarrays are:
less: [ ]
equal: [ -1 ]
greater: [ 0 ]
The less array is empty because there was no value smaller than -1; the other arrays contain a single element each. That means we’re done at this level of the recursion, and we go back up to sort the previous greater array.
That greater array was:
[ 3, 2, 5 ]
This works just the same way as before: we pick the middle element 2 as the pivot and fill up the subarrays:
less: [ ]
equal: [ 2 ]
greater: [ 3, 5 ]
Note that here it would have been better to pick 3 as the pivot – we would have been done sooner. But now we have to recurse into the greater array again to make sure it is sorted. This is why picking a good pivot is important. When you pick too many “bad” pivots, quicksort actually becomes really slow. More on that below.
When we partition the greater subarray, we find:
less: [ 3 ]
equal: [ 5 ]
greater: [ ]
And now we’re done at this level of the recursion because we can’t split up the arrays any further.
This process repeats until all the subarrays have been sorted. In a picture:
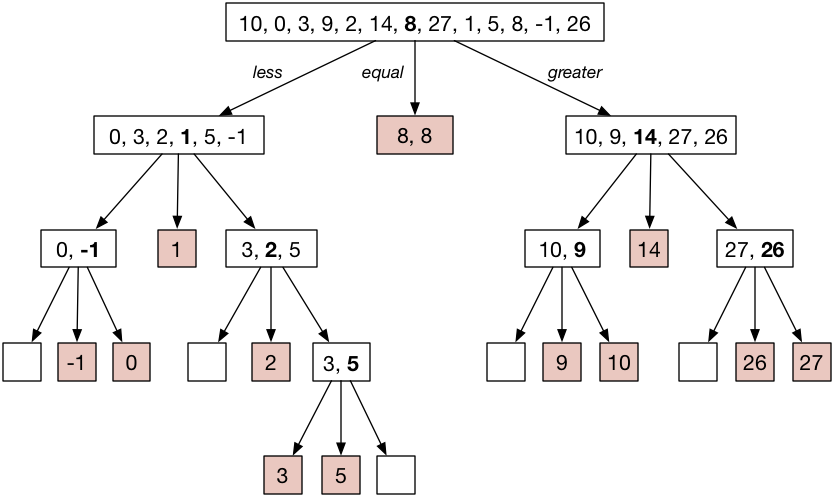
Now if you read the colored boxes from left to right, you get the sorted array:
[ -1, 0, 1, 2, 3, 5, 8, 8, 9, 10, 14, 26, 27 ]
This shows that 8 was a good initial pivot because it appears in the middle of the sorted array too.
I hope this makes the basic principle clear of how quicksort works. Unfortunately, this version of quicksort isn’t very quick, because we filter() the same array three times. There are more clever ways to split up the array.
Partitioning
Dividing the array around the pivot is called partitioning and there are a few different partitioning schemes.
If the array is,
[ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
and we choose the middle element 8 as a pivot then after partitioning the array will look like this:
[ 0, 3, 2, 1, 5, -1, 8, 8, 10, 9, 14, 27, 26 ]
----------------- -----------------
all elements < 8 all elements > 8
The key thing to realize is that after partitioning the pivot element is in its final sorted place already. The rest of the numbers are not sorted yet, they are simply partitioned around the pivot value. Quicksort partitions the array many times over, until all the values are in their final places.
There is no guarantee that partitioning keeps the elements in the same relative order, so after partitioning around pivot 8 you could also end up with something like this:
[ 3, 0, 5, 2, -1, 1, 8, 8, 14, 26, 10, 27, 9 ]
The only guarantee is that to the left of the pivot are all the smaller elements and to the right are all the larger elements. Because partitioning can change the original order of equal elements, quicksort does not produce a “stable” sort (unlike merge sort, for example). Most of the time that’s not a big deal.
Lomuto’s partitioning scheme
In the first example of quicksort I showed you, partitioning was done by calling Swift’s filter() function three times. That is not very efficient. So let’s look at a smarter partitioning algorithm that works in place, i.e. by modifying the original array.
Here’s an implementation of Lomuto’s partitioning scheme in Swift:
func partitionLomuto<T: Comparable>(_ a: inout [T], low: Int, high: Int) -> Int {
let pivot = a[high]
var i = low
for j in low..<high {
if a[j] <= pivot {
(a[i], a[j]) = (a[j], a[i])
i += 1
}
}
(a[i], a[high]) = (a[high], a[i])
return i
}
To test this in a playground, do:
var list = [ 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1, 8 ]
let p = partitionLomuto(&list, low: 0, high: list.count - 1)
list // show the results
Note that list needs to be a var because partitionLomuto() directly changes the contents of the array (it is passed as an inout parameter). That is much more efficient than allocating a new array object.
The low and high parameters are necessary because when this is used inside quicksort, you don’t always want to (re)partition the entire array, only a limited range that becomes smaller and smaller.
Previously we used the middle array element as the pivot but it’s important to realize that the Lomuto algorithm always uses the last element, a[high], for the pivot. Because we’ve been pivoting around 8 all this time, I swapped the positions of 8 and 26 in the example so that 8 is at the end of the array and is used as the pivot value here too.
After partitioning, the array looks like this:
[ 0, 3, 2, 1, 5, 8, -1, 8, 9, 10, 14, 26, 27 ]
*
The variable p contains the return value of the call to partitionLomuto() and is 7. This is the index of the pivot element in the new array (marked with a star).
The left partition goes from 0 to p-1 and is [ 0, 3, 2, 1, 5, 8, -1 ]. The right partition goes from p+1 to the end, and is [ 9, 10, 14, 26, 27 ] (the fact that the right partition is already sorted is a coincidence).
You may notice something interesting… The value 8 occurs more than once in the array. One of those 8s did not end up neatly in the middle but somewhere in the left partition. That’s a small downside of the Lomuto algorithm as it makes quicksort slower if there are a lot of duplicate elements.
So how does the Lomuto algorithm actually work? The magic happens in the for loop. This loop divides the array into four regions:
a[low...i]contains all values <= pivota[i+1...j-1]contains all values > pivota[j...high-1]are values we haven’t looked at yeta[high]is the pivot value
In ASCII art the array is divided up like this:
[ values <= pivot | values > pivot | not looked at yet | pivot ]
low i i+1 j-1 j high-1 high
The loop looks at each element from low to high-1 in turn. If the value of the current element is less than or equal to the pivot, it is moved into the first region using a swap.
Note: In Swift, the notation
(x, y) = (y, x)is a convenient way to perform a swap between the values ofxandy. You can also writeswap(&x, &y).
After the loop is over, the pivot is still the last element in the array. So we swap it with the first element that is greater than the pivot. Now the pivot sits between the <= and > regions and the array is properly partitioned.
Let’s step through the example. The array we’re starting with is:
[| 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
low high
i
j
Initially, the “not looked at” region stretches from index 0 to 11. The pivot is at index 12. The “values <= pivot” and “values > pivot” regions are empty, because we haven’t looked at any values yet.
Look at the first value, 10. Is this smaller than the pivot? No, skip to the next element.
[| 10 | 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
low high
i
j
Now the “not looked at” region goes from index 1 to 11, the “values > pivot” region contains the number 10, and “values <= pivot” is still empty.
Look at the second value, 0. Is this smaller than the pivot? Yes, so swap 10 with 0 and move i ahead by one.
[ 0 | 10 | 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
low high
i
j
Now “not looked at” goes from index 2 to 11, “values > pivot” still contains 10, and “values <= pivot” contains the number 0.
Look at the third value, 3. This is smaller than the pivot, so swap it with 10 to get:
[ 0, 3 | 10 | 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
low high
i
j
The “values <= pivot” region is now [ 0, 3 ]. Let’s do one more… 9 is greater than the pivot, so simply skip ahead:
[ 0, 3 | 10, 9 | 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
low high
i
j
Now the “values > pivot” region contains [ 10, 9 ]. If we keep going this way, then eventually we end up with:
[ 0, 3, 2, 1, 5, 8, -1 | 27, 9, 10, 14, 26 | 8 ]
low high
i j
The final thing to do is to put the pivot into place by swapping a[i] with a[high]:
[ 0, 3, 2, 1, 5, 8, -1 | 8 | 9, 10, 14, 26, 27 ]
low high
i j
And we return i, the index of the pivot element.
Note: If you’re still not entirely clear on how the algorithm works, I suggest you play with this in the playground to see exactly how the loop creates these four regions.
Let’s use this partitioning scheme to build quicksort. Here’s the code:
func quicksortLomuto<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
if low < high {
let p = partitionLomuto(&a, low: low, high: high)
quicksortLomuto(&a, low: low, high: p - 1)
quicksortLomuto(&a, low: p + 1, high: high)
}
}
This is now super simple. We first call partitionLomuto() to reorder the array around the pivot (which is always the last element from the array). And then we call quicksortLomuto() recursively to sort the left and right partitions.
Try it out:
var list = [ 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1, 8 ]
quicksortLomuto(&list, low: 0, high: list.count - 1)
Lomuto’s isn’t the only partitioning scheme but it’s probably the easiest to understand. It’s not as efficient as Hoare’s scheme, which requires fewer swap operations.
Hoare’s partitioning scheme
This partitioning scheme is by Hoare, the inventor of quicksort.
Here is the code:
func partitionHoare<T: Comparable>(_ a: inout [T], low: Int, high: Int) -> Int {
let pivot = a[low]
var i = low - 1
var j = high + 1
while true {
repeat { j -= 1 } while a[j] > pivot
repeat { i += 1 } while a[i] < pivot
if i < j {
a.swapAt(i, j)
} else {
return j
}
}
}
To test this in a playground, do:
var list = [ 8, 0, 3, 9, 2, 14, 10, 27, 1, 5, 8, -1, 26 ]
let p = partitionHoare(&list, low: 0, high: list.count - 1)
list // show the results
Note that with Hoare’s scheme, the pivot is always expected to be the first element in the array, a[low]. Again, we’re using 8 as the pivot element.
The result is:
[ -1, 0, 3, 8, 2, 5, 1, 27, 10, 14, 9, 8, 26 ]
Note that this time the pivot isn’t in the middle at all. Unlike with Lomuto’s scheme, the return value is not necessarily the index of the pivot element in the new array.
Instead, the array is partitioned into the regions [low...p] and [p+1...high]. Here, the return value p is 6, so the two partitions are [ -1, 0, 3, 8, 2, 5, 1 ] and [ 27, 10, 14, 9, 8, 26 ].
The pivot is placed somewhere inside one of the two partitions, but the algorithm doesn’t tell you which one or where. If the pivot value occurs more than once, then some instances may appear in the left partition and others may appear in the right partition.
Because of these differences, the implementation of Hoare’s quicksort is slightly different:
func quicksortHoare<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
if low < high {
let p = partitionHoare(&a, low: low, high: high)
quicksortHoare(&a, low: low, high: p)
quicksortHoare(&a, low: p + 1, high: high)
}
}
I’ll leave it as an exercise for the reader to figure out exactly how Hoare’s partitioning scheme works. :-)
Picking a good pivot
Lomuto’s partitioning scheme always chooses the last array element for the pivot. Hoare’s scheme uses the first element. But there is no guarantee that these pivots are any good.
Here is what happens when you pick a bad value for the pivot. Let’s say the array is,
[ 7, 6, 5, 4, 3, 2, 1 ]
and we’re using Lomuto’s scheme. The pivot is the last element, 1. After pivoting, we have the following arrays:
less than pivot: [ ]
equal to pivot: [ 1 ]
greater than pivot: [ 7, 6, 5, 4, 3, 2 ]
Now recursively partition the “greater than” subarray and get:
less than pivot: [ ]
equal to pivot: [ 2 ]
greater than pivot: [ 7, 6, 5, 4, 3 ]
And again:
less than pivot: [ ]
equal to pivot: [ 3 ]
greater than pivot: [ 7, 6, 5, 4 ]
And so on…
That’s no good, because this pretty much reduces quicksort to the much slower insertion sort. For quicksort to be efficient, it needs to split the array into roughly two halves.
The optimal pivot for this example would have been 4, so we’d get:
less than pivot: [ 3, 2, 1 ]
equal to pivot: [ 4 ]
greater than pivot: [ 7, 6, 5 ]
You might think this means we should always choose the middle element rather than the first or the last, but imagine what happens in the following situation:
[ 7, 6, 5, 1, 4, 3, 2 ]
Now the middle element is 1 and that gives the same lousy results as in the previous example.
Ideally, the pivot is the median element of the array that you’re partitioning, i.e. the element that sits in the middle of the sorted array. Of course, you won’t know what the median is until after you’ve sorted the array, so this is a bit of a chicken-and-egg problem. However, there are some tricks to choose good, if not ideal, pivots.
One trick is “median-of-three”, where you find the median of the first, middle, and last element in this subarray. In theory that often gives a good approximation of the true median.
Another common solution is to choose the pivot randomly. Sometimes this may result in choosing a suboptimal pivot but on average this gives very good results.
Here is how you can do quicksort with a randomly chosen pivot:
func quicksortRandom<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
if low < high {
let pivotIndex = random(min: low, max: high) // 1
(a[pivotIndex], a[high]) = (a[high], a[pivotIndex]) // 2
let p = partitionLomuto(&a, low: low, high: high)
quicksortRandom(&a, low: low, high: p - 1)
quicksortRandom(&a, low: p + 1, high: high)
}
}
There are two important differences with before:
-
The
random(min:max:)function returns an integer in the rangemin...max, inclusive. This is our pivot index. -
Because the Lomuto scheme expects
a[high]to be the pivot entry, we swapa[pivotIndex]witha[high]to put the pivot element at the end before callingpartitionLomuto().
It may seem strange to use random numbers in something like a sorting function, but it is necessary to make quicksort behave efficiently under all circumstances. With bad pivots, the performance of quicksort can be quite horrible, O(n^2). But if you choose good pivots on average, for example by using a random number generator, the expected running time becomes O(n log n), which is as good as sorting algorithms get.
Dutch national flag partitioning
But there are more improvements to make! In the first example of quicksort I showed you, we ended up with an array that was partitioned like this:
[ values < pivot | values equal to pivot | values > pivot ]
But as you’ve seen with the Lomuto partitioning scheme, if the pivot occurs more than once the duplicates end up in the left half. And with Hoare’s scheme the pivot can be all over the place. The solution to this is “Dutch national flag” partitioning, named after the fact that the Dutch flag has three bands just like we want to have three partitions.
The code for this scheme is:
func partitionDutchFlag<T: Comparable>(_ a: inout [T], low: Int, high: Int, pivotIndex: Int) -> (Int, Int) {
let pivot = a[pivotIndex]
var smaller = low
var equal = low
var larger = high
while equal <= larger {
if a[equal] < pivot {
swap(&a, smaller, equal)
smaller += 1
equal += 1
} else if a[equal] == pivot {
equal += 1
} else {
swap(&a, equal, larger)
larger -= 1
}
}
return (smaller, larger)
}
This works very similarly to the Lomuto scheme, except that the loop partitions the array into four (possibly empty) regions:
[low ... smaller-1]contains all values < pivot[smaller ... equal-1]contains all values == pivot[equal ... larger]contains all values > pivot[larger ... high]are values we haven’t looked at yet
Note that this doesn’t assume the pivot is in a[high]. Instead, you have to pass in the index of the element you wish to use as a pivot.
An example of how to use it:
var list = [ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
partitionDutchFlag(&list, low: 0, high: list.count - 1, pivotIndex: 10)
list // show the results
Just for fun, we’re giving it the index of the other 8 this time. The result is:
[ -1, 0, 3, 2, 5, 1, 8, 8, 27, 14, 9, 26, 10 ]
Notice how the two 8s are in the middle now. The return value from partitionDutchFlag() is a tuple, (6, 7). This is the range that contains the pivot value(s).
Here is how you would use it in quicksort:
func quicksortDutchFlag<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
if low < high {
let pivotIndex = random(min: low, max: high)
let (p, q) = partitionDutchFlag(&a, low: low, high: high, pivotIndex: pivotIndex)
quicksortDutchFlag(&a, low: low, high: p - 1)
quicksortDutchFlag(&a, low: q + 1, high: high)
}
}
Using Dutch flag partitioning makes for a more efficient quicksort if the array contains many duplicate elements. (And I’m not just saying that because I’m Dutch!)
Note: The above implementation of
partitionDutchFlag()uses a customswap()routine for swapping the contents of two array elements. Unlike Swift’s ownswap(), this doesn’t give an error when the two indices refer to the same array element. See Quicksort.swift for the code.
See also
Written for Swift Algorithm Club by Matthijs Hollemans