Rootish Array Stack

A Rootish Array Stack is an ordered array based structure that minimizes wasted space (based on Gauss’s summation technique). A Rootish Array Stack consists of an array holding many fixed size arrays in ascending size.

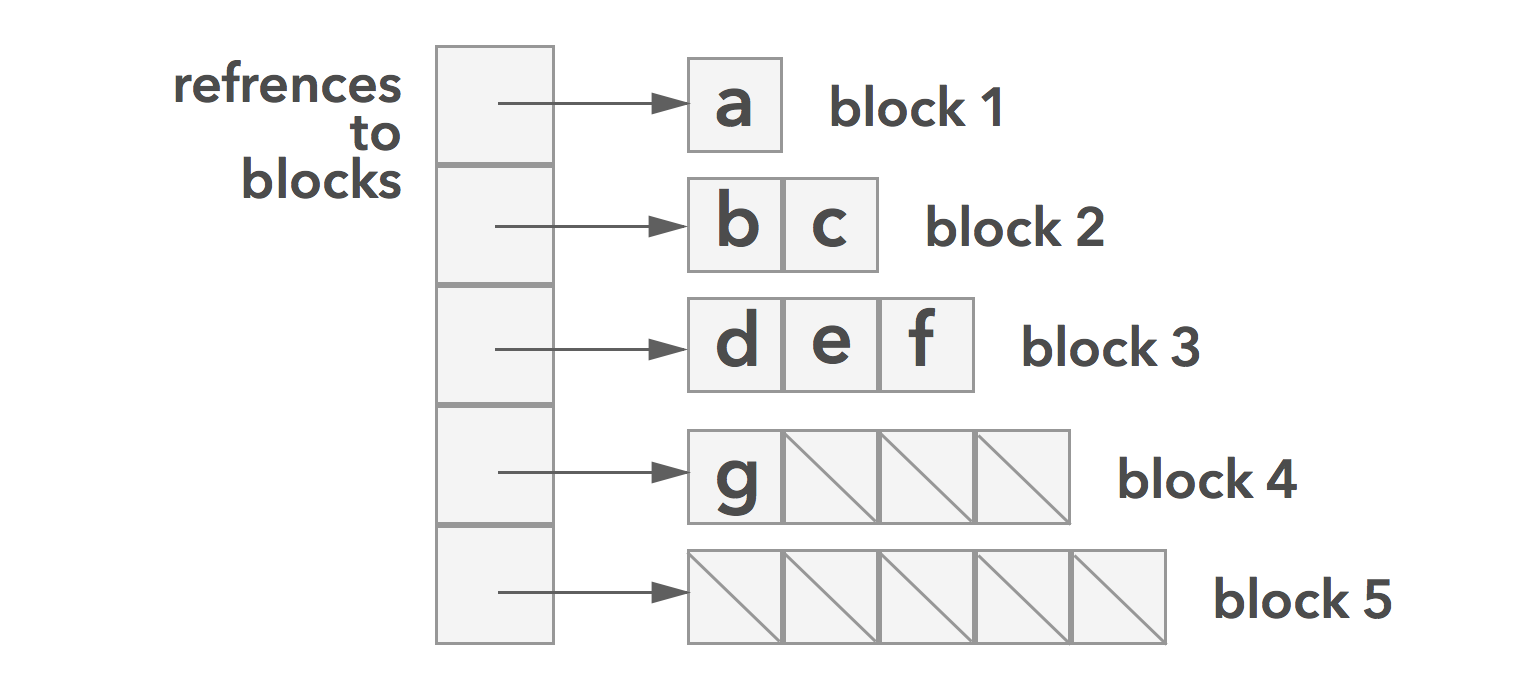
A resizable array holds references to blocks (arrays of fixed size). A block’s capacity is the same as it’s index in the resizable array. Blocks don’t grow/shrink like regular Swift arrays. Instead, when their capacity is reached, a new slightly larger block is created. When a block is emptied the last block is freed. This is a great improvement on what Swift arrays do in terms of wasted space.

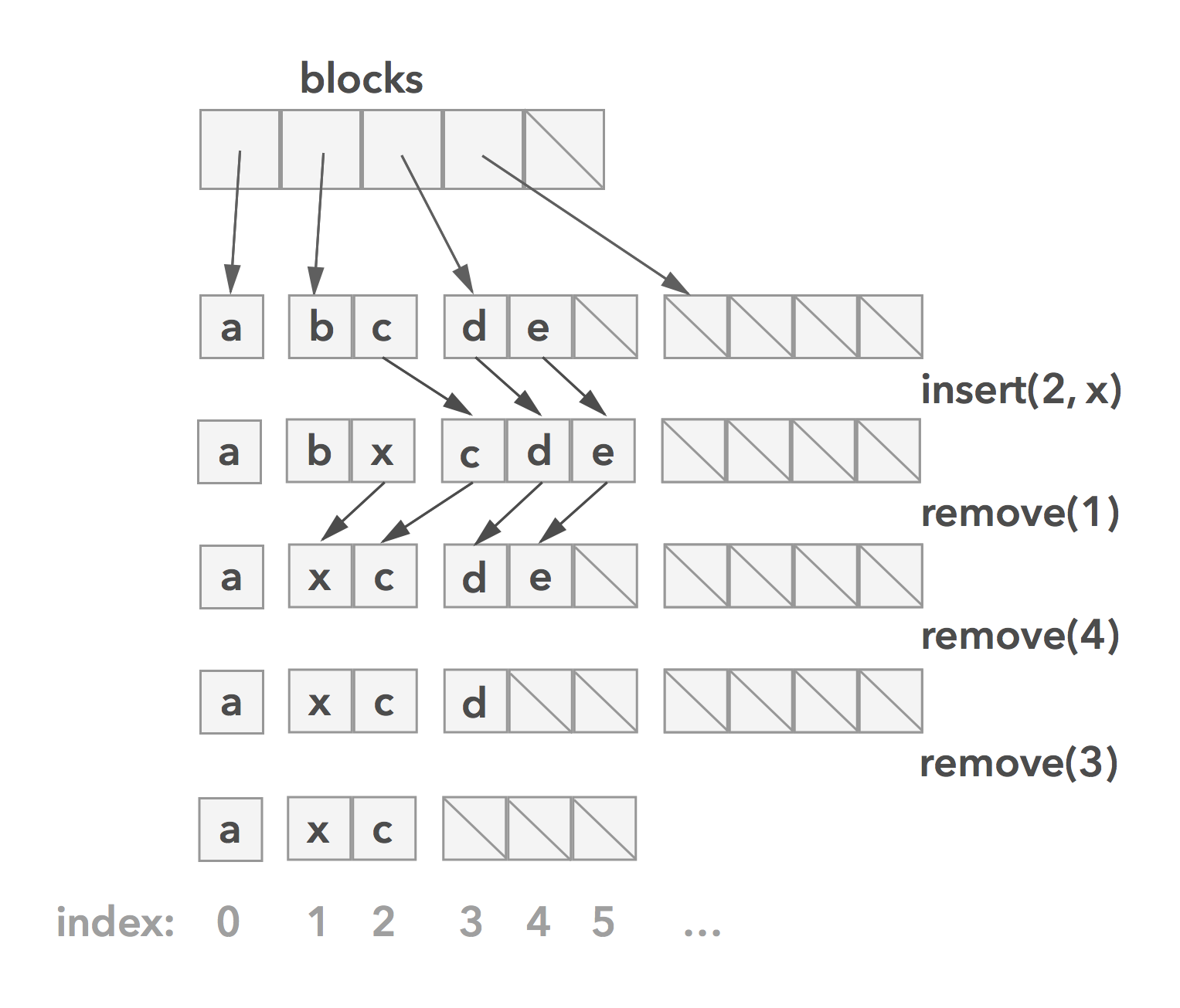
Here you can see how insert/remove operations would behave (very similar to how a Swift array handles such operations).

Gauss’ Summation Trick

One of the most well known legends about famous mathematician Carl Friedrich Gauss goes back to when he was in primary school. One day, Gauss’ teacher asked his class to add up all the numbers from 1 to 100, hoping that the task would take long enough for him to step out for a smoke break. The teacher was shocked when young Gauss had his hand up with the answer 5050. So soon? The teacher suspected a cheat, but no. Gauss had found a formula to sidestep the problem of manually adding up all the numbers 1 by 1. His formula:

sum from 1...n = n * (n + 1) / 2

To understand this imagine n blocks where x represents 1 unit. In this example let n be 5:

blocks:     [x] [x x] [x x x] [x x x x] [x x x x x]
# of x's:    1    2      3        4          5

Block 1 has 1 x, block 2 as 2 xs, block 3 has 3 xs, etc…

If you wanted to take the sum of all the blocks from 1 to n, you could go through and count them one by one. This is okay, but for a large sequence of blocks that could take a long time! Instead, you could arrange the blocks to look like a half pyramid:

# |  blocks
--|-------------
1 |  x
2 |  x x
3 |  x x x
4 |  x x x x
5 |  x x x x x

Then we mirror the half pyramid and rearrange the image so that it fits with the original half pyramid in a rectangular shape:

x                  o      x o o o o o
x x              o o      x x o o o o
x x x          o o o  =>  x x x o o o
x x x x      o o o o      x x x x o o
x x x x x  o o o o o      x x x x x o

Here we have n rows and n + 1 columns. 5 rows and 6 columns.

We can calculate the sum just as we would an area! Let’s also express the width and height in terms of n:

area of a rectangle = height * width = n * (n + 1)

We only want to calculate the amount of xs, not the amount of os. Since there’s a 1:1 ratio between xs and os we can just divide our area by 2!

area of only x = n * (n + 1) / 2

Voila! A super fast way to take a sum of all the blocks! This equation is useful for deriving fast block and inner block index equations.

Get/Set with Speed

Next, we want to find an efficient and accurate way to access an element at a random index. For example, which block does rootishArrayStack[12] point to? To answer this we will need more math! Determining the inner block index turns out to be easy. If index is in some block then:

inner block index = index - block * (block + 1) / 2

Determining which block an index points to is more difficult. The number of elements up to and including the element requested is: index + 1 elements. The number of elements in blocks 0...block is (block + 1) * (block + 2) / 2 (equation derived above). The relationship between the block and the index is as follows:

(block + 1) * (block + 2) / 2 >= index + 1

This can be rewritten as:

(block)^2 + (3 * block) - (2 * index) >= 0

Using the quadratic formula we get:

block = (-3 ± √(9 + 8 * index)) / 2

A negative block doesn’t make sense, so we take the positive root instead. In general, this solution is not an integer. However, going back to our inequality, we want the smallest block such that block => (-3 + √(9 + 8 * index)) / 2. Next, we take the ceiling of the result:

block = ⌈(-3 + √(9 + 8 * index)) / 2⌉

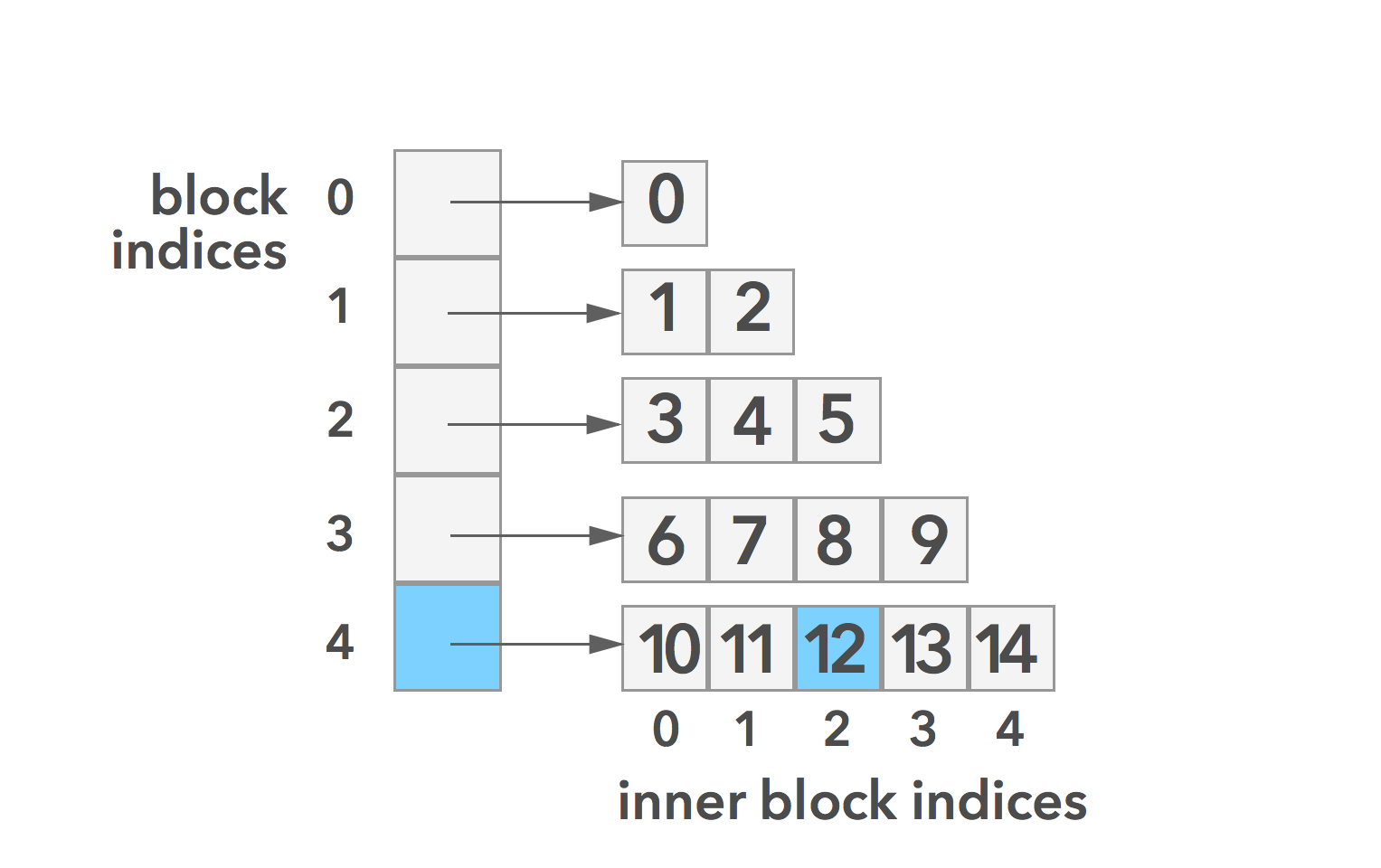
Now we can figure out what rootishArrayStack[12] points to! First, let’s see which block the 12 points to:

block = ⌈(-3 + √(9 + 8 * (12))) / 2⌉
block = ⌈(-3 + √105) / 2⌉
block = ⌈(-3 + (10.246950766)) / 2⌉
block = ⌈(7.246950766) / 2⌉
block = ⌈3.623475383⌉
block = 4

Next lets see which innerBlockIndex 12 points to:

inner block index = (12) - (4) * ((4) + 1) / 2
inner block index = (12) - (4) * (5) / 2
inner block index = (12) - 10
inner block index = 2

Therefore, rootishArrayStack[12] points to the block at index 4 and at inner block index 2.

Interesting Discovery

Using the block equation, we can see that the number of blocks is proportional to the square root of the number of elements: O(blocks) = O(√n).

Implementation Details

Let’s start with instance variables and struct declaration:

import Darwin

public struct RootishArrayStack<T> {

  fileprivate var blocks = [Array<T?>]()
  fileprivate var internalCount = 0

  public init() { }

  var count: Int {
    return internalCount
  }

  ...

}

The elements are of generic type T, so data of any kind can be stored in the list. blocks will be a resizable array to hold fixed sized arrays that take type T?.

The reason for the fixed size arrays taking type T? is so that references to elements aren’t retained after they’ve been removed. Eg: if you remove the last element, the last index must be set to nil to prevent the last element being held in memory at an inaccessible index.

internalCount is an internal mutable counter that keeps track of the number of elements. count is a read only variable that returns the internalCount value. Darwin is imported here to provide simple math functions such as ceil() and sqrt().

The capacity of the structure is simply the Gaussian summation trick:

var capacity: Int {
  return blocks.count * (blocks.count + 1) / 2
}

Next, let’s look at how we would get and set elements:

fileprivate func block(fromIndex: Int) -> Int {
  let block = Int(ceil((-3.0 + sqrt(9.0 + 8.0 * Double(index))) / 2))
  return block
}

fileprivate func innerBlockIndex(fromIndex index: Int, fromBlock block: Int) -> Int {
  return index - block * (block + 1) / 2
}

public subscript(index: Int) -> T {
  get {
    let block = self.block(fromIndex: index)
    let innerBlockIndex = self.innerBlockIndex(fromIndex: index, fromBlock: block)
    return blocks[block][innerBlockIndex]!
  }
  set(newValue) {
    let block = self.block(fromIndex: index)
    let innerBlockIndex = self.innerBlockIndex(fromIndex: index, fromBlock: block)
    blocks[block][innerBlockIndex] = newValue
  }
}

block(fromIndex:) and innerBlockIndex(fromIndex:, fromBlock:) are wrapping the block and inner block index equations we derived earlier. superscript lets us have get and set access to the structure with the familiar [index:] syntax. For both get and set in superscript we use the same logic:

1. determine the block that the index points to
2. determine the inner block index
3. get/set the value

Next, let’s look at how we would growIfNeeded() and shrinkIfNeeded().

fileprivate mutating func growIfNeeded() {
  if capacity - blocks.count < count + 1 {
    let newArray = [T?](repeating: nil, count: blocks.count + 1)
    blocks.append(newArray)
  }
}

fileprivate mutating func shrinkIfNeeded() {
  if capacity + blocks.count >= count {
    while blocks.count > 0 && (blocks.count - 2) * (blocks.count - 1) / 2 >    count {
      blocks.remove(at: blocks.count - 1)
    }
  }
}

If our data set grows or shrinks in size, we want our data structure to accommodate the change. Just like a Swift array, when a capacity threshold is met we will grow or shrink the size of our structure. For the Rootish Array Stack we want to grow if the second last block is full on an insert operation, and shrink if the two last blocks are empty.

Now to the more familiar Swift array behaviour.

public mutating func insert(element: T, atIndex index: Int) {
	growIfNeeded()
	internalCount += 1
	var i = count - 1
	while i > index {
		self[i] = self[i - 1]
		i -= 1
	}
	self[index] = element
}

public mutating func append(element: T) {
	insert(element: element, atIndex: count)
}

public mutating func remove(atIndex index: Int) -> T {
	let element = self[index]
	for i in index..<count - 1 {
		self[i] = self[i + 1]
	}
	internalCount -= 1
	makeNil(atIndex: count)
	shrinkIfNeeded()
	return element
}

fileprivate mutating func makeNil(atIndex index: Int) {
  let block = self.block(fromIndex: index)
  let innerBlockIndex = self.innerBlockIndex(fromIndex: index, fromBlock: block)
  blocks[block][innerBlockIndex] = nil
}

To insert(element:, atIndex:) we move all elements after the index to the right by 1. After space has been made for the element, we set the value using the subscript convenience method. append(element:) is just a convenience method to insert to the end. To remove(atIndex:) we move all the elements after the index to the left by 1. After the removed value is covered by it’s proceeding value, we set the last value in the structure to nil. makeNil(atIndex:) uses the same logic as our subscript method but is used to set the root optional at a particular index to nil (because setting it’s wrapped value to nil is something only the user of the data structure should do).

Setting a optionals value to nil is different than setting it’s wrapped value to nil. An optionals wrapped value is an embedded type within the optional reference. This means that a nil wrapped value is actually .some(.none) whereas setting the root reference to nil is .none. To better understand Swift optionals I recommend checking out @SebastianBoldt’s article Swift! Optionals?.

Performance

• An internal counter keeps track of the number of elements in the structure. count is executed in O(1) time.

• capacity can be calculated using Gauss’ summation trick in an equation which takes O(1) time to execute.

• Since subcript[index:] uses the block and inner block index equations, which can be executed in O(1) time, all get and set operations take O(1).

• Ignoring the time cost to grow and shrink, insert(atIndex:) and remove(atIndex:) operations shift all elements right of the specified index resulting in O(n) time.

Analysis of Growing and Shrinking

The performance analysis doesn’t account for the cost to grow and shrink. Unlike a regular Swift array, grow and shrink operations don’t copy all the elements into a backing array. They only allocate or free an array proportional to the number of blocks. The number of blocks is proportional to the square root of the number of elements. Growing and shrinking only costs O(√n).

Wasted Space

Wasted space is how much memory with respect to the number of elements n is unused. The Rootish Array Stack never has more than 2 empty blocks and it never has less than 1 empty block. The last two blocks are proportional to the number of blocks, which is proportional to the square root of the number of elements. The number of references needed to point to each block is the same as the number of blocks. Therefore, the amount of wasted space with respect to the number of elements is O(√n).

Written for Swift Algorithm Club by @BenEmdon

With help from OpenDataStructures.org