Shortest Path (Unweighted Graph)
Goal: find the shortest route to go from one node to another in a graph.
Suppose we have to following graph:
/Images/Graph.png)
We may want to find out what the shortest way is to get from node A to node F.
If the graph is unweighed, then finding the shortest path is easy: we can use the breadth-first search algorithm. For a weighted graph, we can use Dijkstra’s algorithm.
Unweighted graph: breadth-first search
Breadth-first search is a method for traversing a tree or graph data structure. It starts at a source node and explores the immediate neighbor nodes first, before moving to the next level neighbors. As a convenient side effect, it automatically computes the shortest path between a source node and each of the other nodes in the tree or graph.
The result of the breadth-first search can be represented with a tree:
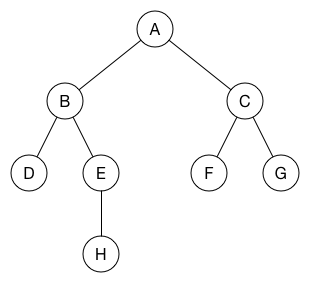
The root of the tree is the node you started the breadth-first search from. To find the distance from node A to any other node, we simply count the number of edges in the tree. And so we find that the shortest path between A and F is 2. The tree not only tells you how long that path is, but also how to actually get from A to F (or any of the other nodes).
Let’s put breadth-first search into practice and calculate the shortest path from A to all the other nodes. We start with the source node A and add it to a queue with a distance of 0.
queue.enqueue(element: A)
A.distance = 0
The queue is now [ A ]. We dequeue A and enqueue its two immediate neighbor nodes B and C with a distance of 1.
queue.dequeue() // A
queue.enqueue(element: B)
B.distance = A.distance + 1 // result: 1
queue.enqueue(element: C)
C.distance = A.distance + 1 // result: 1
The queue is now [ B, C ]. Dequeue B and enqueue B’s neighbor nodes D and E with a distance of 2.
queue.dequeue() // B
queue.enqueue(element: D)
D.distance = B.distance + 1 // result: 2
queue.enqueue(element: E)
E.distance = B.distance + 1 // result: 2
The queue is now [ C, D, E ]. Dequeue C and enqueue C’s neighbor nodes F and G, also with a distance of 2.
queue.dequeue() // C
queue.enqueue(element: F)
F.distance = C.distance + 1 // result: 2
queue.enqueue(element: G)
G.distance = C.distance + 1 // result: 2
This continues until the queue is empty and we’ve visited all the nodes. Each time we discover a new node, it gets the distance of its parent plus 1. As you can see, this is exactly what the breadth-first search algorithm does, except that we now also keep track of the distance travelled.
Here’s the code:
func breadthFirstSearchShortestPath(graph: Graph, source: Node) -> Graph {
let shortestPathGraph = graph.duplicate()
var queue = Queue<Node>()
let sourceInShortestPathsGraph = shortestPathGraph.findNodeWithLabel(label: source.label)
queue.enqueue(element: sourceInShortestPathsGraph)
sourceInShortestPathsGraph.distance = 0
while let current = queue.dequeue() {
for edge in current.neighbors {
let neighborNode = edge.neighbor
if !neighborNode.hasDistance {
queue.enqueue(element: neighborNode)
neighborNode.distance = current.distance! + 1
}
}
}
return shortestPathGraph
}
Put this code in a playground and test it like so:
let shortestPathGraph = breadthFirstSearchShortestPath(graph: graph, source: nodeA)
print(shortestPathGraph.nodes)
This will output:
Node(label: a, distance: 0), Node(label: b, distance: 1), Node(label: c, distance: 1),
Node(label: d, distance: 2), Node(label: e, distance: 2), Node(label: f, distance: 2),
Node(label: g, distance: 2), Node(label: h, distance: 3)
Note: This version of
breadthFirstSearchShortestPath()does not actually produce the tree, it only computes the distances. See minimum spanning tree on how you can convert the graph into a tree by removing edges.
Written by Chris Pilcher and Matthijs Hollemans