Skip List
Skip List is a probablistic data-structure with same logarithmic time bound and efficiency as AVL/ or Red-Black tree and provides a clever compromise to efficiently support search and update operations and is relatively simpler to implement compared to other map data structures.
A skip list S consists of series of sorted linked lists {L0, …, Ln}, layered hierarchicaly and each layer L stores a subset of items in layer L0 in incremental order. The items in layers {L1, … Ln} are chosen at random based on a coin flipping function with probability 1/2 . For traversing, every item in a layer hold references to the node below and the next node. This layers serve as express lanes to the layer underneath them, effectively making fast O(log n) searching possible by skipping lanes and reducing travel distance and in worse case searching degrades to O (n), as expected with regular linked list.
For a skip list S:
- List L0 contains every inserted item.
- For lists {L1, …, Ln}, Li contains a randomly generated subset of the items in Li-1
- Height is determined by coin-flipping.
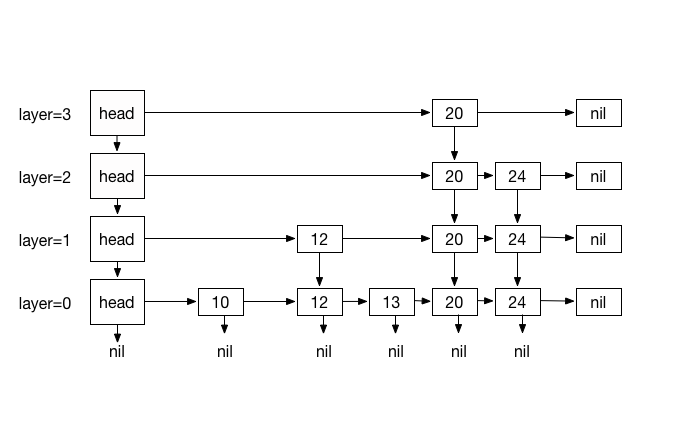 Figure 1
Figure 1
#Searching
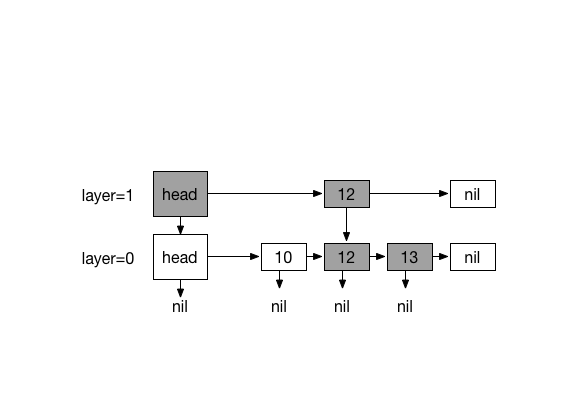
Searching for element N starts by traversing from top most layer Ln until L0.
Our objective is to find an element K such that its value at the rightmost
position of current layer, is less-than target item and its subsequent node has
a greater-equal value or nil ( K.key < N.key <= (K.next.key or nil) ). if
value of K.next is equal to N, search is terminated and we return K.next,
otherwise drop underneath using K.down to the node below ( at layer Ln-1 ) and
repeat the process until L0 where K.down is nil which indicates that level
is L0 and item doesn’t exists.
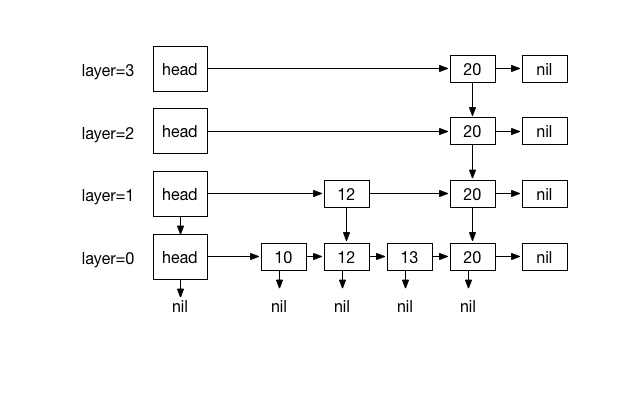
###Example:
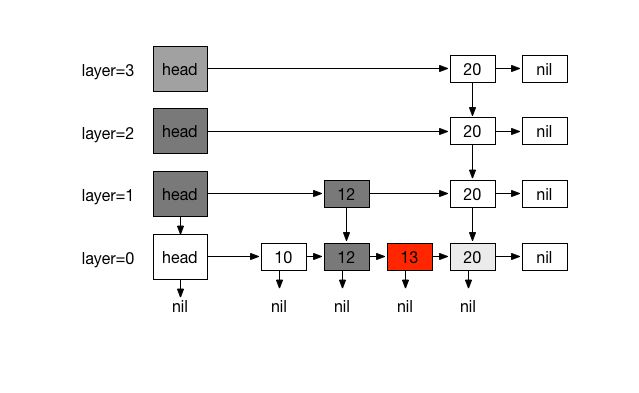
#Inserting
Inserting element N has a similar process as searching. It starts by traversing from top most layer Ln until L0. We need to keep track of our traversal path using a stack. It helps us to traverse the path upward when coin-flipping starts, so we can insert our new element and update references to it.
Our objective is to find a element K such that its value at the rightmost
position of layer Ln, is less-than new item and its subsequent node has a
greater-equal value or nil ( K.key < N.key < (K.next.key or nil) ). Push
element K to the stack and with element K, go down using K.down to the
node below ( at layer Ln-1 ) and repeat the process ( forward searching ) up
until L0 where K.down is nil which indicates that level is L0. We
terminate the process when K.down is nil.
At L0, N can be inserted after K.
Here is the interesting part. We use coin flipping function to randomly create layers.
When coin flip function returns 0, the whole process is finished but when returns 1, there are two possibilities:
- Stack is empty ( Level is L0 /- Ln or at uninitialized stage)
- Stack has items ( traversing upward is possible )
In case 1:
A new layer M* is created with a head node NM referencing head node of layer below and NM.next referencing new element N. New element N referecing element N at previous layer.
In case 2:
repeat until stack is empty Pop an item F from stack and update the references accordingly. F.next will be K.next and K.next will be F
when stack is empty Create a new layer consisintg of a head node NM referencing head node of layer below and NM.next referencing new element N. New element N referencing element N at previous layer.
###Example:
Inserting 13. with coin flips (0)
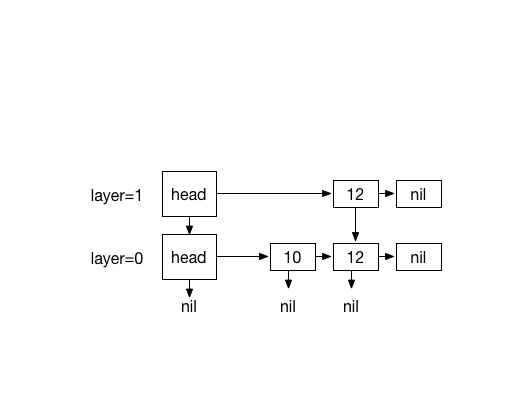
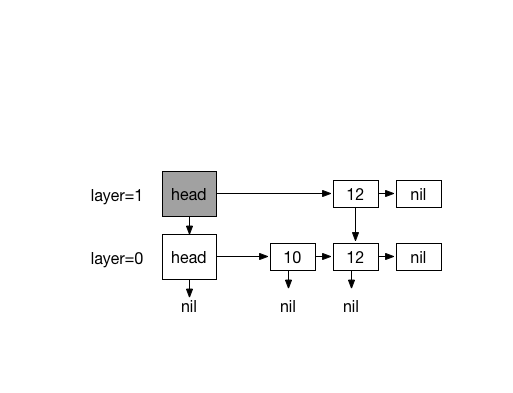
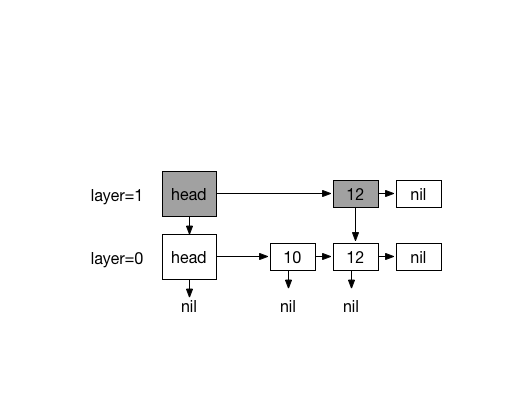
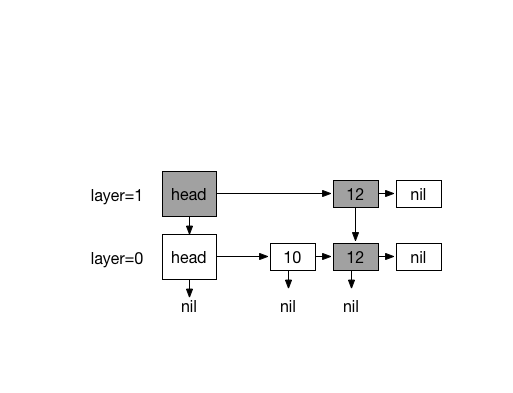
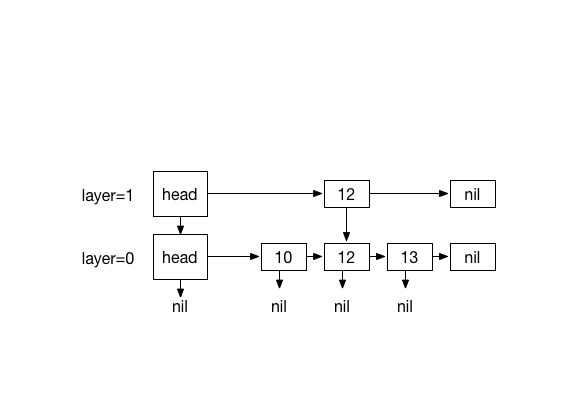
Inserting 20. with 4 times coin flips (1)

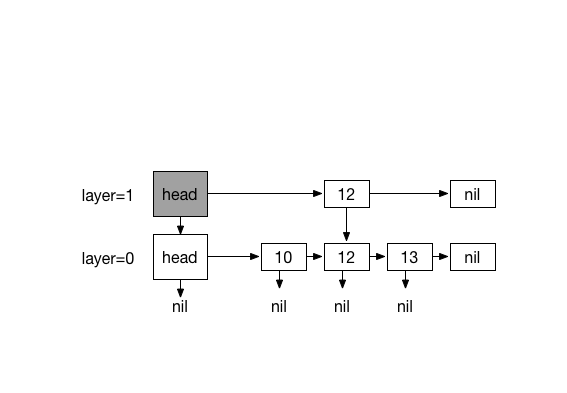
#Removing
Removing works similar to insert procedure.
TODO
#See also
Written for Swift Algorithm Club by Mike Taghavi