Threaded Binary Tree
A threaded binary tree is a special kind of binary tree (a tree in which each node has at most two children) that maintains a few extra variables to allow cheap and fast in-order traversal of the tree. We will explore the general structure of threaded binary trees, as well as the Swift implementation of a fully functioning threaded binary tree.
If you don’t know what a tree is or what it is for, then read this first.
In-order traversal
The main motivation behind using a threaded binary tree over a simpler and smaller standard binary tree is to increase the speed of an in-order traversal of the tree. An in-order traversal of a binary tree visits the nodes in the order in which they are stored, which matches the underlying ordering of a binary search tree. This means most threaded binary trees are also binary search trees. The idea is to visit all the left children of a node first, then visit the node itself, and then visit the right children last.
An in-order traversal of any binary tree generally goes as follows (using Swift syntax):
func traverse(n: Node?) {
if (n == nil) { return
} else {
traverse(n.left)
visit(n)
traverse(n.right)
}
}
Where n is a a node in the tree (or nil), each node stores its children as
left and right, and “visiting” a node can mean performing any desired
action on it. We would call this function by passing to it the root of the
tree we wish to traverse.
While simple and understandable, this algorithm uses stack space proportional to the height of the tree due to its recursive nature. If the tree has n nodes, this usage can range anywhere from O(log n) for a fairly balanced tree, to O(n) to a very unbalanced tree.
A threaded binary tree fixes this problem.
For more information about in-order traversals see here.
Predecessors and successors
An in-order traversal of a tree yields a linear ordering of the nodes. Thus
each node has both a predecessor and a successor (except for the first
and last nodes, which only have a successor or a predecessor respectively). In
a threaded binary tree, each left child that would normally be nil instead
stores the node’s predecessor (if it exists), and each right child that would
normally be nil instead stores the node’s successor (if it exists). This is
what separates threaded binary trees from standard binary trees.
There are two types of threaded binary trees: single threaded and double threaded:
- A single threaded tree keeps track of either the in-order predecessor or successor (left or right).
- A double threaded tree keeps track of both the in-order predecessor and successor (left and right).
Using a single or double threaded tree depends on what we want to accomplish. If we only need to traverse the tree in one direction (either forward or backward), then we use a single threaded tree. If we want to traverse in both directions, then we use a double threaded tree.
It is important to note that each node stores either its predecessor or its left child, and either its successor or its right child. The nodes do not need to keep track of both. For example, in a double threaded tree, if a node has a right child but no left child, it will track its predecessor in place of its left child.
Here is an example valid “full” threaded binary tree:
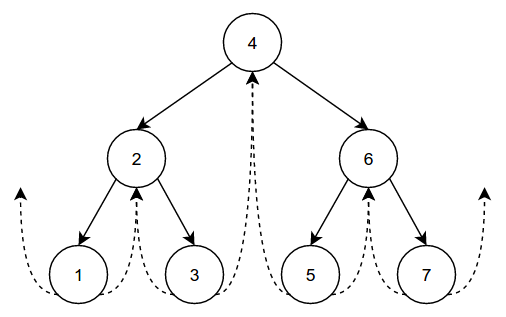
While the following threaded binary tree is not “full,” it is still valid. The structure of the tree does not matter as long as it follows the definition of a binary search tree:
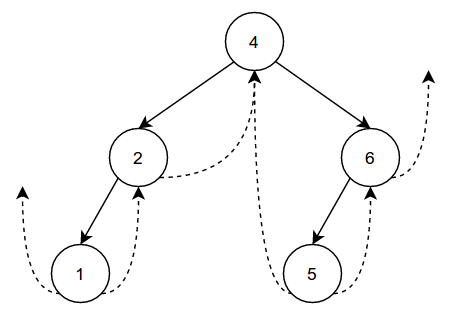
The solid lines denote the links between parents and children, while the dotted lines denote the “threads.” It is important to note how the children and thread edges interact with each other. Every node besides the root has one entering edge (from its parent), and two leaving edges: one to the left and one to the right. The left leaving edge goes to the node’s left child if it exists, and to its in-order predecessor if it does not. The right leaving edge goes to the node’s right child if it exists, and to its in-order successor if it does not. The exceptions are the left-most node and the right-most node, which do not have a predecessor or successor, respectively.
Representation
Before we go into detail about the methods of a threaded binary tree, we should
first explain how the tree itself is represented. The core of this data
structure is the ThreadedBinaryTree<T: Comparable> class. Each instance of
this class represents a node with six member variables: value, parent,
left, right, leftThread, and rightThread. Of all of these, only
value is required. The other five are Swift optionals (they may be nil).
value: Tis the value of this node (e.g. 1, 2, A, B, etc.)parent: ThreadedBinaryTree?is the parent of this nodeleft: ThreadedBinaryTree?is the left child of this noderight: ThreadedBinaryTree?is the right child of this nodeleftThread: ThreadedBinaryTree?is the in-order predecessor of this noderightThread: ThreadedBinaryTree?is the in-order successor of this node
As we are storing both leftThread and rightThread, this is a double
threaded tree. Now we are ready to go over some of the member functions in our
ThreadedBinaryTree class.
Traversal algorithm
Let’s start with the main reason we’re using a threaded binary tree. It is now
very easy to find the in-order predecessor and the in-order successor of any
node in the tree. If the node has no left/right child, we can simply
return the node’s leftThread/rightThread. Otherwise, it is trivial to move
down the tree and find the correct node.
func predecessor() -> ThreadedBinaryTree<T>? {
if let left = left {
return left.maximum()
} else {
return leftThread
}
}
func successor() -> ThreadedBinaryTree<T>? {
if let right = right {
return right.minimum()
} else {
return rightThread
}
}
Note:
maximum()andminimum()are methods ofThreadedBinaryTreewhich return the largest/smallest node in a given sub-tree. See the implementation for more detail.
Because these are ThreadedBinaryTree methods, we can call
node.predecessor() or node.successor() to obtain the predecessor or
successor of any node, provided that node is a ThreadedBinaryTree object.
Because predecessors and/or successors are tracked, an in-order traversal of a threaded binary tree is much more efficient than the recursive algorithm outlined above. We use these predecessor/successor attributes to great effect in this new algorithm for both forward and backward traversals:
public func traverseInOrderForward(_ visit: (T) -> Void) {
var n: ThreadedBinaryTree
n = minimum()
while true {
visit(n.value)
if let successor = n.successor() {
n = successor
} else {
break
}
}
}
public func traverseInOrderBackward(_ visit: (T) -> Void) {
var n: ThreadedBinaryTree
n = maximum()
while true {
visit(n.value)
if let predecessor = n.predecessor() {
n = predecessor
} else {
break
}
}
}
Again, this a method of ThreadedBinaryTree, so we’d call it via
node.traverseInorderForward(visitFunction). Note that we are able to specify
a function that executes on each node as they are visited. This function can
be anything you want, as long as it accepts T (the type of the values of the
nodes of the tree) and has no return value.
Let’s walk through a forward traversal of a tree by hand to get a better idea of how a computer would do it. For example, take this simple threaded tree:
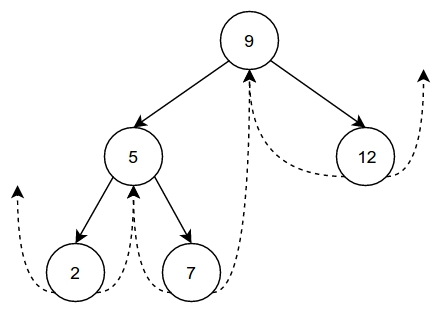
We start at the root of the tree, 9. Note that we don’t visit(9) yet.
From there we want to go to the minimum() node in the tree, which is 2 in
this case. We then visit(2) and see that it has a rightThread, and thus
we immediately know what its successor() is. We follow the thread to 5,
which does not have any leaving threads. Therefore, after we visit(5), we go
to the minimum() node in its right subtree, which is 7. We then
visit(7) and see that it has a rightThread, which we follow to get back to
9. Now we visit(9), and after noticing that it has no rightThread,
we go to the minimum() node in its right subtree, which is 12. This
node has a rightThread that leads to nil, which signals that we have
completed the traversal! We visited the nodes in order 2, 5, 7, 9, 12,
which intuitively makes sense, as that is their natural increasing order.
A backward traversal would be very similar, but you would replace right,
rightThread, minimum(), and successor() with left, leftThread,
maximum(), and predecessor().
Insertion and deletion
The quick in-order traversal that a threaded binary trees gives us comes at a
small cost. Inserting/deleting nodes becomes more complicated, as we have to
continuously manage the leftThread and rightThread variables. Rather than
walking through some boring code, it is best to explain this with an example
(although you can read through the implementation
if you want to know the finer details). Please note that this requires
knowledge of binary search trees, so make sure you have
read this first.
Note: we do allow duplicate nodes in this implementation of a threaded binary tree. We break ties by defaulting insertion to the right.
Let’s start with the same tree that we used for the above traversal example:

Suppose we insert 10 into this tree. The resulting graph would look like this, with the changes highlighted in red:
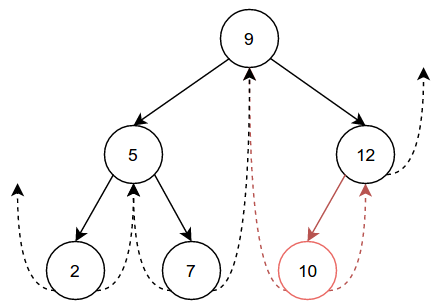
If you’ve done your homework and are familiar with binary search trees, the
placement of this node should not surprise you. What’s new is how we maintain
the threads between nodes. So we know that we want to insert 10 as
12’s left child. The first thing we do is set 12’s left child to
10, and set 10’s parent to 12. Because 10 is being inserted
on the left, and 10 has no children of its own, we can safely set
10’s rightThread to its parent 12. What about 10’s
leftThread? Because we know that 10 < 12, and 10 is the only
left child of 12, we can safely set 10’s leftThread to 12’s
(now outdated) leftThread. Finally we set 12’s leftThread = nil, as it
now has a left child.
Let’s now insert another node, 4, into the tree:
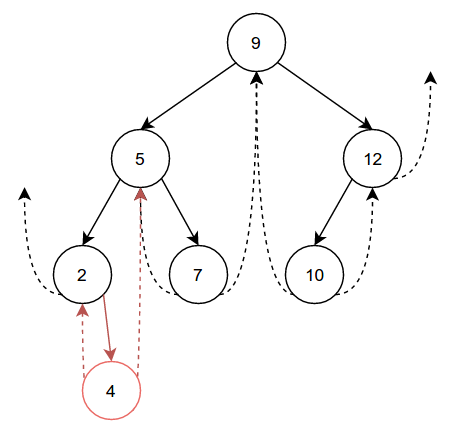
While we are inserting 4 as a right child, it follows the exact same
process as above, but mirrored (swap left and right). For the sake of
completeness, we’ll insert one final node, 15:
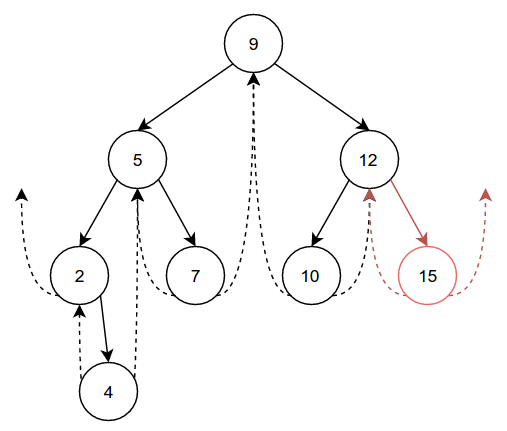
Now that we have a fairly crowded tree, let’s try removing some nodes. Compared to insertion, deletion is a little more complicated. Let’s start with something simple, like removing 7, which has no children:
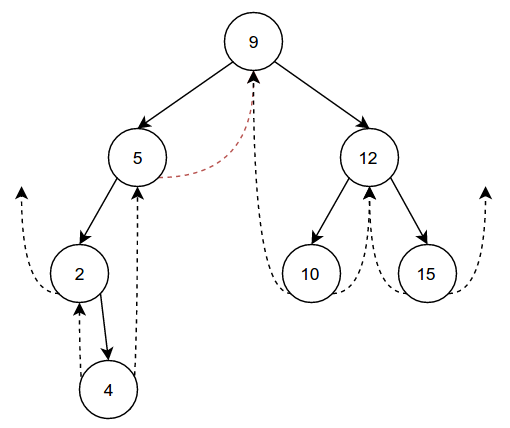
Before we can just throw 7 away, we have to perform some clean-up. In this
case, because 7 is a right child and has no children itself, we can
simply set the rightThread of 7’s parent(5) to 7’s (now
outdated) rightThread. Then we can just set 7’s parent, left,
right, leftThread, and rightThread to nil, effectively removing it from
the tree. We also set the parent’s rightChild to nil, which completes the deletion of this right child.
Let’s try something a little harder. Say we remove 5 from the tree:
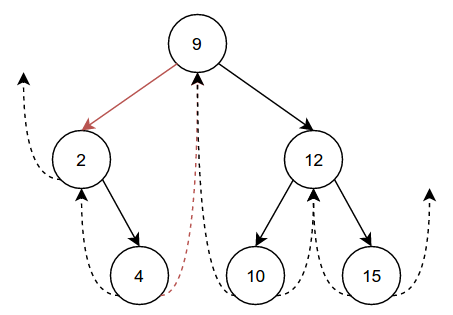
This is a little trickier, as 5 has some children that we have to deal
with. The core idea is to replace 5 with its first child, 2. To
accomplish this, we of course set 2’s parent to 9 and set 9’s
left child to 2. Note that 4’s rightThread used to be 5, but
we are removing 5, so it needs to change. It is now important to
understand two important properties of threaded binary trees:
- For the rightmost node m in the
leftsubtree of any node n, m’srightThreadis n. - For the leftmost node m in the
rightsubtree of any node n, m’sleftThreadis n.
Note how these properties held true before the removal of 5, as 4 was
the rightmost node in 5’s left subtree. In order to maintain this
property, we must set 4’s rightThread to 9, as 4 is now the
rightmost node in 9’s left subtree. To completely remove 5, all we
now have to do is set 5’s parent, left, right, leftThread, and
rightThread to nil.
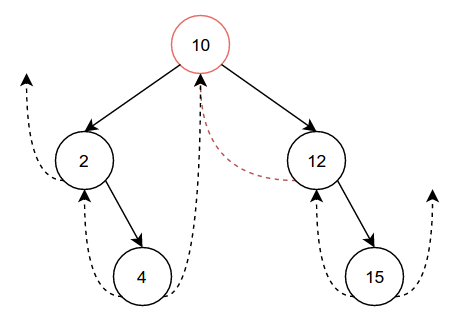
How about we do something crazy? What would happen if we tried to remove 9, the root node? This is the resulting tree:
Whenever we want to remove a node that has two children, we take a slightly
different approach than the above examples. The basic idea is to replace the
node that we want to remove with the leftmost node in its right subtree,
which we call the replacement node.
Note: we could also replace the node with the rightmost node in its
leftsubtree. Choosing left or right is mostly an arbitrary decision.
Once we find the replacement node, 10 in this case, we remove it from the
tree using the algorithms outlined above. This ensures that the edges in the
right subtree remain correct. From there it is easy to replace 9 with
10, as we just have to update the edges leaving 10. Now all we have to
do is fiddle with the threads in order to maintain the two properties outlined
above. In this case, 12’s leftThread is now 10. Node 9 is no
longer needed, so we can finish the removal process by setting all of its
variables to nil.
In order to illustrate how to remove a node that has only a right child,
we’ll remove one final node, 12 from the tree:
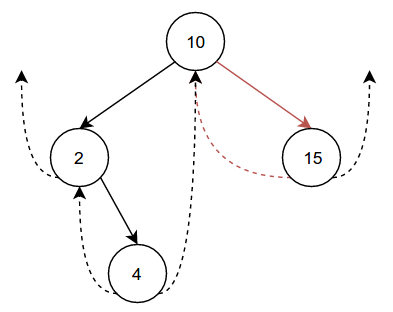
The process to remove 12 is identical to the process we used to remove
5, but mirrored. 5 had a left child, while 12 has a right
child, but the core algorithm is the same.
And that’s it! This was just a quick overview of how insertion and deletion work in threaded binary trees, but if you understood these examples, you should be able to insert or remove any node from any tree you want. More detail can of course be found in the implementation.
Miscellaneous methods
There are many other smaller operations that a threaded binary tree can do,
such as searching() for a node in the tree, finding the depth() or
height() of a node, etc. You can check
the implementation for the full technical details.
Many of these methods are inherent to binary search trees as well, so you can
find further documentation here.
See also
Threaded Binary Tree on Wikipedia
Written for the Swift Algorithm Club by Jayson Tung Migrated to Swift 3 by Jaap Wijnen
Images made using www.draw.io