Trees

This topic has been tutorialized here

A tree represents hierarchical relationships between objects. This is a tree:

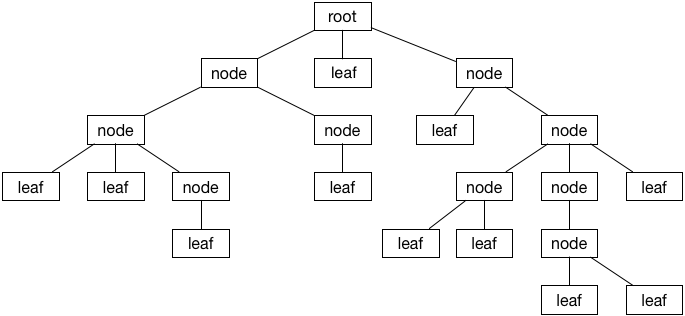
A tree consists of nodes, and these nodes are linked to one another.

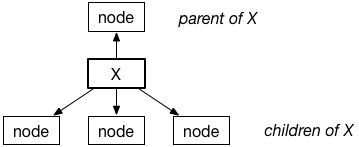
Nodes have links to their children and usually to their parent as well. The children are the nodes below a given node; the parent is the node above. A node always has just one parent but can have multiple children.

A node without a parent is the root node. A node without children is a leaf node.

The pointers in a tree do not form cycles. This is not a tree:

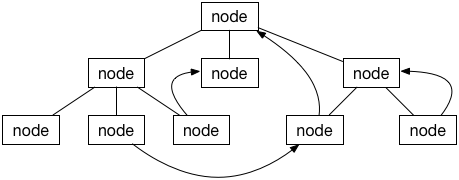
Such a structure is called a graph. A tree is really a very simple form of a graph. (In a similar vein, a linked list is a simple version of a tree. Think about it!)

This article talks about a general-purpose tree. That’s a tree without any kind of restrictions on how many children each node may have, or on the order of the nodes in the tree.

Here’s a basic implementation in Swift:

public class TreeNode<T> {
  public var value: T

  public weak var parent: TreeNode?
  public var children = [TreeNode<T>]()

  public init(value: T) {
    self.value = value
  }

  public func addChild(_ node: TreeNode<T>) {
    children.append(node)
    node.parent = self
  }
}

This describes a single node from the tree. It has a value of generic type T, a reference to a parent node, and an array of child nodes.

It will be useful to add a description method so you can print the tree:

extension TreeNode: CustomStringConvertible {
  public var description: String {
    var s = "\(value)"
    if !children.isEmpty {
      s += " {" + children.map { $0.description }.joined(separator: ", ") + "}"
    }
    return s
  }
}

To see this in action in a playground:

let tree = TreeNode<String>(value: "beverages")

let hotNode = TreeNode<String>(value: "hot")
let coldNode = TreeNode<String>(value: "cold")

let teaNode = TreeNode<String>(value: "tea")
let coffeeNode = TreeNode<String>(value: "coffee")
let chocolateNode = TreeNode<String>(value: "cocoa")

let blackTeaNode = TreeNode<String>(value: "black")
let greenTeaNode = TreeNode<String>(value: "green")
let chaiTeaNode = TreeNode<String>(value: "chai")

let sodaNode = TreeNode<String>(value: "soda")
let milkNode = TreeNode<String>(value: "milk")

let gingerAleNode = TreeNode<String>(value: "ginger ale")
let bitterLemonNode = TreeNode<String>(value: "bitter lemon")

tree.addChild(hotNode)
tree.addChild(coldNode)

hotNode.addChild(teaNode)
hotNode.addChild(coffeeNode)
hotNode.addChild(chocolateNode)

coldNode.addChild(sodaNode)
coldNode.addChild(milkNode)

teaNode.addChild(blackTeaNode)
teaNode.addChild(greenTeaNode)
teaNode.addChild(chaiTeaNode)

sodaNode.addChild(gingerAleNode)
sodaNode.addChild(bitterLemonNode)

If you print out the value of tree, you’ll get:

beverages {hot {tea {black, green, chai}, coffee, cocoa}, cold {soda {ginger ale, bitter lemon}, milk}}

That corresponds to the following structure:

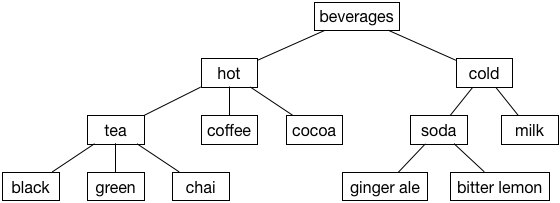
The beverages node is the root because it has no parent. The leaves are black, green, chai, coffee, cocoa, ginger ale, bitter lemon, milk because they don’t have any child nodes.

For any node you can look at the parent property and work your way back up to the root:

teaNode.parent           // this is the "hot" node
teaNode.parent!.parent   // this is the root

We often use the following definitions when talking about trees:

• Height of the tree. This is the number of links between the root node and the lowest leaf. In our example the height of the tree is 3 because it takes three jumps to go from the root to the bottom.

• Depth of a node. The number of links between this node and the root node. For example, the depth of tea is 2 because it takes two jumps to reach the root. (The root itself has depth 0.)

There are many different ways to construct trees. For example, sometimes you don’t need to have a parent property at all. Or maybe you only need to give each node a maximum of two children – such a tree is called a binary tree. A very common type of tree is the binary search tree (or BST), a stricter version of a binary tree where the nodes are ordered in a particular way to speed up searches.

The general purpose tree I’ve shown here is great for describing hierarchical data, but it really depends on your application what kind of extra functionality it needs to have.

Here’s an example of how you could use the TreeNode class to determine if the tree contains a particular value. You first look at the node’s own value property. If there’s no match, then you look at all your children in turn. Of course, those children are also TreeNodes so they will repeat the same process recursively: first look at their own value and then at their children. And their children will also do the same thing again, and so on… Recursion and trees go hand-in-hand.

Here’s the code:

extension TreeNode where T: Equatable {
  func search(_ value: T) -> TreeNode? {
    if value == self.value {
      return self
    }
    for child in children {
      if let found = child.search(value) {
        return found
      }
    }
    return nil
  }
}

And an example of how to use this:

tree.search("cocoa")    // returns the "cocoa" node
tree.search("chai")     // returns the "chai" node
tree.search("bubbly")   // nil

It’s also possible to describe a tree using nothing more than an array. The indices in the array then create the links between the different nodes. For example, if we have:

0 = beverage		5 = cocoa		9  = green
1 = hot			6 = soda		10 = chai
2 = cold		7 = milk		11 = ginger ale
3 = tea			8 = black		12 = bitter lemon
4 = coffee				

Then we can describe the tree with the following array:

[ -1, 0, 0, 1, 1, 1, 2, 2, 3, 3, 3, 6, 6 ]

Each entry in the array is a pointer to its parent node. The item at index 3, tea, has the value 1 because its parent is hot. The root node points to -1 because it has no parent. You can only traverse such trees from a node back to the root but not the other way around.

By the way, sometimes you see algorithms using the term forest. Unsurprisingly, that is the name given to a collection of separate tree objects. For an example of this, see union-find.

Written for Swift Algorithm Club by Matthijs Hollemans