Trie

This topic has been tutorialized here

What is a Trie?

A Trie, (also known as a prefix tree, or radix tree in some other implementations) is a special type of tree used to store associative data structures. A Trie for a dictionary might look like this:

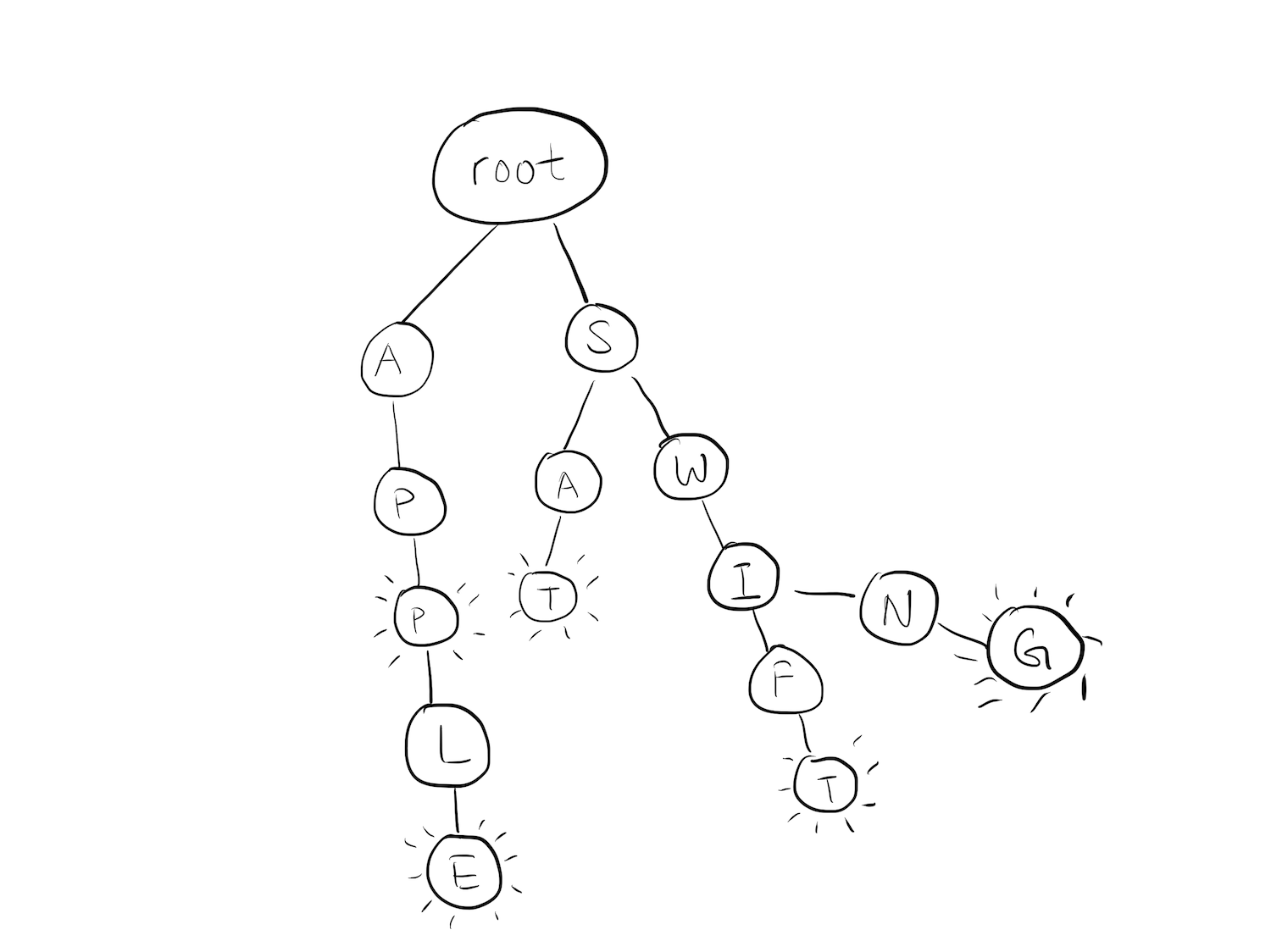
Storing the English language is a primary use case for a Trie. Each node in the Trie would represent a single character of a word. A series of nodes then make up a word.

Why a Trie?

Tries are very useful for certain situations. Here are some of the advantages:

• Looking up values typically have a better worst-case time complexity.
• Unlike a hash map, a Trie does not need to worry about key collisions.
• Doesn’t utilize hashing to guarantee a unique path to elements.
• Trie structures can be alphabetically ordered by default.

Common Algorithms

Contains (or any general lookup method)

Trie structures are great for lookup operations. For Trie structures that model the English language, finding a particular word is a matter of a few pointer traversals:

func contains(word: String) -> Bool {
  guard !word.isEmpty else { return false }

  // 1
  var currentNode = root
  
  // 2
  var characters = Array(word.lowercased())
  var currentIndex = 0
 
  // 3
  while currentIndex < characters.count, 
    let child = currentNode.children[characters[currentIndex]] {

    currentNode = child
    currentIndex += 1
  }

  // 4
  if currentIndex == characters.count && currentNode.isTerminating {
    return true
  } else {
    return false
  }
}

The contains method is fairly straightforward:

1. Create a reference to the root. This reference will allow you to walk down a chain of nodes.
2. Keep track of the characters of the word you’re trying to match.
3. Walk the pointer down the nodes.
4. isTerminating is a boolean flag for whether or not this node is the end of a word. If this if condition is satisfied, it means you are able to find the word in the trie.

Insertion

Insertion into a Trie requires you to walk over the nodes until you either halt on a node that must be marked as terminating, or reach a point where you need to add extra nodes.

func insert(word: String) {
  guard !word.isEmpty else {
    return
  }

  // 1
  var currentNode = root

  // 2
  for character in word.lowercased() {
    // 3
    if let childNode = currentNode.children[character] {
      currentNode = childNode
    } else {
      currentNode.add(value: character)
      currentNode = currentNode.children[character]!
    }
  }
  // Word already present?
  guard !currentNode.isTerminating else {
    return
  }

  // 4
  wordCount += 1
  currentNode.isTerminating = true
}

1. Once again, you create a reference to the root node. You’ll move this reference down a chain of nodes.
2. Begin walking through your word letter by letter
3. Sometimes, the required node to insert already exists. That is the case for two words inside the Trie that shares letters (i.e “Apple”, “App”). If a letter already exists, you’ll reuse it, and simply traverse deeper down the chain. Otherwise, you’ll create a new node representing the letter.
4. Once you get to the end, you mark isTerminating to true to mark that specific node as the end of a word.

Removal

Removing keys from the trie is a little tricky, as there are a few more cases you’ll need to take into account. Nodes in a Trie may be shared between different words. Consider the two words “Apple” and “App”. Inside a Trie, the chain of nodes representing “App” is shared with “Apple”.

If you’d like to remove “Apple”, you’ll need to take care to leave the “App” chain in tact.

func remove(word: String) {
  guard !word.isEmpty else {
    return
  }

  // 1
  guard let terminalNode = findTerminalNodeOf(word: word) else {
    return
  }

  // 2
  if terminalNode.isLeaf {
    deleteNodesForWordEndingWith(terminalNode: terminalNode)
  } else {
    terminalNode.isTerminating = false
  }
  wordCount -= 1
}

1. findTerminalNodeOf traverses through the Trie to find the last node that represents the word. If it is unable to traverse through the chain of characters, it returns nil.
2. deleteNodesForWordEndingWith traverse backwords, deleting the nodes represented by the word.

Time Complexity

Let n be the length of some value in the Trie.

• contains - Worst case O(n)
• insert - O(n)
• remove - O(n)

Other Notable Operations

• count: Returns the number of keys in the Trie - O(1)
• words: Returns a list containing all the keys in the Trie - O(1)
• isEmpty: Returns true if the Trie is empty, false otherwise - O(1)

See also Wikipedia entry for Trie.

Written for the Swift Algorithm Club by Christian Encarnacion. Refactored by Kelvin Lau

Changes by Rick Zaccone

• Added comments to all methods
• Refactored the remove method
• Renamed some variables. I have mixed feelings about the way Swift infers types. It’s not always apparent what type a variable will have. To address this, I made changes such as renaming parent to parentNode to emphasize that it is a node and not the value contained within the node.
• Added a words property that recursively traverses the trie and constructs an array containing all of the words in the trie.
• Added a isLeaf property to TrieNode for readability.
• Implemented count and isEmpty properties for the trie.
• I tried stress testing the trie by adding 162,825 words. The playground was very slow while adding the words and eventually crashed. To fix this problem, I moved everything into a project and wrote XCTest tests that test the trie. There are also several performance tests. Everything passes.